دوستان و همراهان همیگشی سلام، ناصر گاگمی هستم یکی از نویسندههای سایت بخون، با آموزش فصل دو ریاضی نهم همراه شما دوستان هستم. فصل دوم ریاضی نهم، در مورد اعداد حقیقی میباشد. شاید به نظر شما این بحث خیلی تکراری شده باشد، اما درس دوم ریاضی نهم خیلی نکات مهمی را در خود جای داده است. فصل دو ریاضی نهم بسیار پر کاربرد میباشد و همیشه مورد توجه و علاقه طراحان سوالات و آزمونها بوده است، اما امروز قرار است با کاملترین آموزش ریاضی نهم فصل دوم، چیزی برای صحبت باقی نگذاریم. در ضمن از طریق لینک آموزش فصل اول ریاضی نهم، حتما آموزش این فصل را هم مشاهده کنید.
فصل دوم ریاضی نهم، تشکیل شده از اعداد گویا، اعداد حقیقی و همچنین قدر مطلق و کاربردهای آن میباشد که قدر مطلق، مهمترین بحث این فصل میباشد. از این فصل برای امتحانانت نهایی معمولا بین 1/5 نمره تا 2 نمره در نظر گرفته میشود. امیدوارم با نکاتی که در تدریس فصل دوم ریاضی نهم، گفته میشود، نمرات بسیار خوبی را کسب کنید.
شما در تصویر زیر به راحتی میتوانید نقشه راه یادگیری ریاضی نهم اعداد حقیقی را مشاهده کنید.
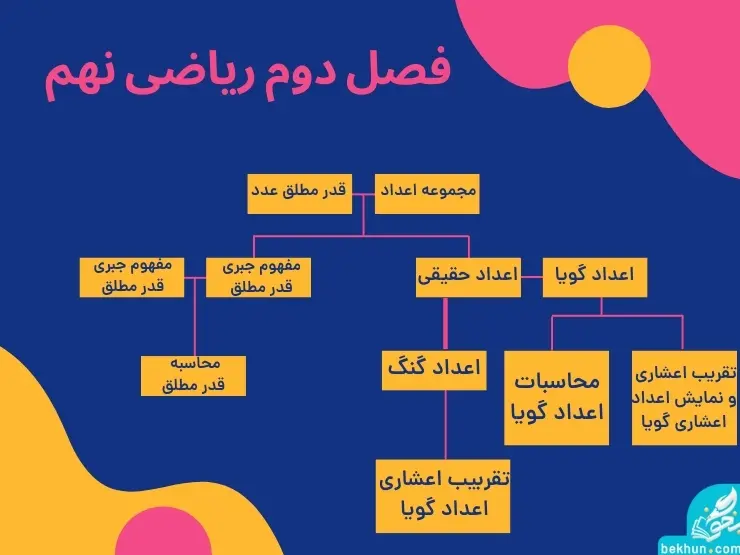
دوستان عزیز به شما پیشنهاد میکنم، پس از به پایان رساندن این مقاله، حتما نمونه سوال فصل دو ریاضی نهم | عددهای حقیقی، را به خوبی مطالعه کنید. تا بتوانید نمره کامل این درس را کسب کنید.
عددهای گویا ریاضی نهم
هر عددی که بتوان آن را بصورت یک کسر نوشت، و صورت و مخرج آن کسر عضوی از اعداد صحیح باشد و مخرج آن هر گز برابر صفر نباشد یک عدد گویا میباشد. پس عدد گویا را بصورت زیر نمایش میدهیم. هر کدام از اعداد زیر نیز یک عدد گویا به شمار میآیند.
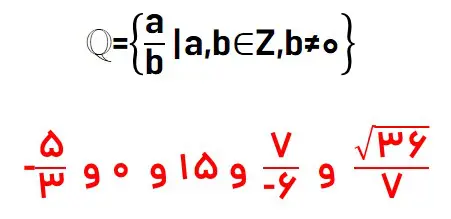
نکته: از آنجایی که میتوان اعداد طبیعی، حسابی و صحیح را با افزودن به مخرج یک به صورت یک کسر نوشت، پس هر یک از اعداد طبیعی، حسابی و صحیح، یک عدد گویا به شمار میآیند.
روش های پیدا کردن عدد های گویا میان دو عدد گویا
برای اینکه بدانیم بین دو عدد گویا، چند عدد گویا دیگر وجود دارد از دو روش:
- یکسان کردن مخرج ها
- روش میانگین
استفاده میکنیم که به بررسی هر کدام از این دو روش در آموزش ریاضی نهم فصل دوم میپردازیم.
روش یکسان کردن مخرج کسرها
در این روش برای پیدا کردن اعداد گویا، در هر مرحله باید مخرجها را یکسان کنیم. به همین منظور صورت و مخرج اعداد گویای داده شده را در اعداد مناسبی ضرب میکنیم تا در هر دو عدد گویا مخرجها یکی شوند. سپس کسری بین این دو عدد گویا خواهد بود که مخرج آن با مخرج دو عدد گویای دیگر یکسان است، و صورت آن عددی است میان دو عدد گویای دیگر. برای راحتتر فهمیدن این روش مثال تصویر زیر را با هم حل خواهیم کرد.
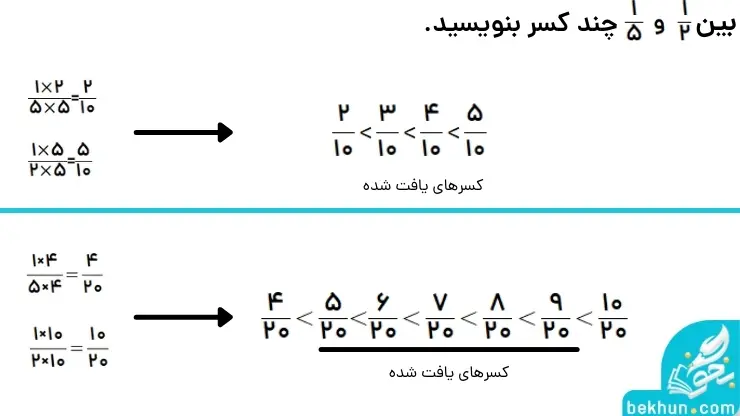
به همین ترتیب تصویر بالا که پیش برویم میتوانیم بیشمار کسر بین این دو عدد گویا پیدا کنیم.
اگر به دنبال گرفتن نمره 20 در درس عربی نهم خود هستید، مقالهی تمرینات عربی نهم با جواب، میتواند شما را بسیار به این نمره نزدیک کند.
روش میانگین
در این روش برای پیدا کردن اعداد گویای میان دو عدد گویای داده شده، باید میانگین دو عدد کسری داده شده را بدست بیاوریم. زیرا همیشه میدانیم که میانگین دو عدد، همیشه عددی است که میان آن دو عدد اصلی قرار دارد. برای راحتتر فهمیدن روش میانگین، مثال تصویر زیر را با هم حل خواهیم کرد.
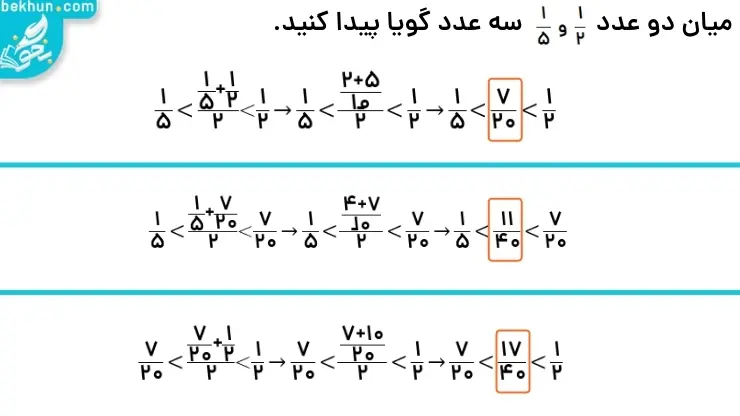
نکته: بین هر دو عدد گویا، میتوان بیشمار کسر پیدا کرد. یا به عبارتی دیگر بین هر دو کسر بینهایت کسر دیگر وجود دارد.
نکته: مجموعه اعداد گویا را نمیتوان با نوشت عضوها نشان داد.
مقایسه کسرها ریاضی نهم
برای مقایسه کردن کسرها و مرتب کردن آنها از بزرگ به کوچک و یا بالعکس، اول از همه باید همه کسرها را هم مخرج کنیم. برای یکسان کردن مخرجها، ک. م. م ( کوچکترین مخرج مشترک) بین مخرجها را بدست میآوریم، سپس صورتها در عدد مناسب ضرب کرده تا یکسان کردن مخرجها به پایان برسد. سپس به مرتب کردن کسرها خواهیم پرداخت. برای اینکه بیشتر با مقایسه کسرها آشنا شوید، مثال تصویر زیر را به خوبی مشاهده کنید.
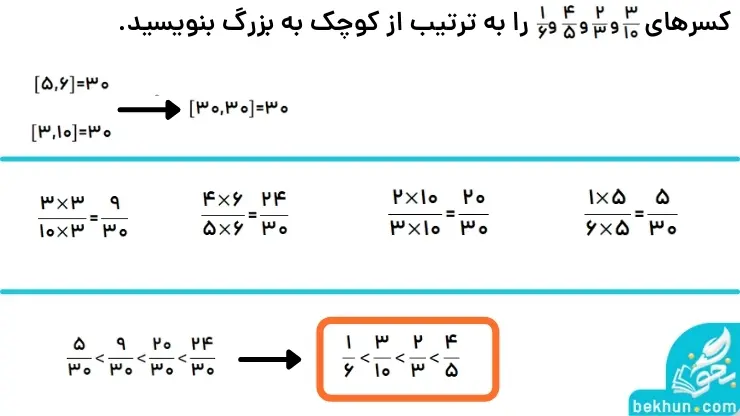
عدد گویای تحویل پذیر
عدد گویای تحولپذیر، عددی است که بتوان صورت و مخرج آنها را ساده کرد یعنی ب. م. م ( بزرگترین مخرج مشترک) صورت و مخرج آنها، عددی بزرگتر از 1 است.
عدد گویای تحویل ناپذیر
عدد گویای تحول ناپذیر، عددی است که صورت و مخرج آن را نمیتوان ساده کرد، یعنی ب. م. م ( بزرگترین مخرج مشترک) صورت و مخرج آنها یک است.
نمایش اعشاری عددهای گویا
اگر عدد موجود روی صورت یک کسر را بر عدد موجود روی مخرج آن تقسیم کنیم، نمایش اعشاری آن کسر بوجود خواهد آمد. برای بهتر فهمیدن این موضوع مثالهای تصویر زیز را با هم حل خواهیم کرد.
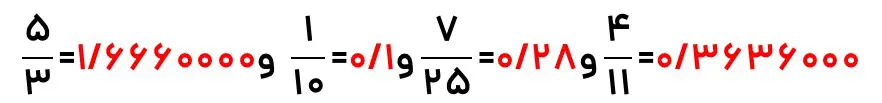
همان گونه که در مثال بالا مشاهده کردید، تعداد ارقام اعشاری هر کسر با کسر دیگر متفاوت است و گاهی این تعداد به بینهایت میرسد. بنابراین نمایش اعشاری عددهای گویا را بر حسب نوع نمایششان میتوان به دستههای زیر تقسیم کرد.
- اعداد اعشاری مختوم یا متناهی
- اعداد اعشاری متناوب ساده
- اعداد اعشاری متناوب مرکب
کلاس نهمیهای عزیز، اگر وقت کافی برای پیدا کردن پاسخ پرسشهای کاروفناوی ندارید، دیگر لازم نیست که نگران این موضوع باشید، ما در مقالهی جواب پرسشهای کار و فناوری نهم، پاسخ تمامی این پرسشها را برای شما قرار دادهایم.
اعداد اعشاری مختوم یا متنهای
اعداد اعشاری مختوم یا متناهی، اعدادی هستند که تعداد رقم های اعشار آنها متنهای است و در یک عدد مشخص پایان مییابد. مانند: 5/486
اعداد اعشاری متناوب ساده
اعداد اعشاری متناوب ساده، اعدادی هستند که در تجزیه مخرج آنها فقط عامل های اول غیر از 2 و 5 وجود داشته باشد. در چنین کسرهایی اگر صورت را بر مخرج تقسیم کنیم، رقم یا ارقامی در در خارج قسمت تکرار میشود. مثل تقسیم 5 بر 3 که برابر است با: 1/666000
اعداد اعشاری متناوب یا مرکب
اعداد اعشاری متناوب یا مرکب، اعدادی هستند که در تجزیه مخرج آنها، عامل های اول 2 یا 5 وجود دارد و در عین حال عامل های دیگری مثل 3 یا 7 یا 11 یا … نیز دیده میشود. در این کسرها اگر صورت را بر مخرج تقسیم کنیم، در خارج قسمت غیر ارقامی که متناوب تکرار میشوند، رقم های دیگری نیز وجود دارد که تکرار نمیشوند. مثل تقسم 4 بر 15 که برابر است با: 0.2666000
اعداد حقیقی ریاضی نهم
ریاضی نهم اعداد حقیقی، درس دوم میباشد که شامل مباحث: اعداد گنگ، نمایش اعداد گنگ روی محور و خود بحث اصلی اعداد حقیقی میباشد.
اعداد گنگ در ریاضی نهم
به عدد هایی مانند رادیکال 11 و رادیکال 5 و 0/231000022…… که تعداد رقم های اعشار آنها بینهایت بوده و دارای دوره تناوب نیستند، اعداد گنگ یا اصم می گویند. و آن را با نماد Q و بک پریم بالای آن نشان میدهند.
مثال: درستی و یا نادرستی هر یک از عبارت های موجود در عکس را مشخص کنید.

پاسخ: موارد ب و پ و ج درست و الف و ت و ث نادرست میباشند.
نکته بسیار مهم: عددی که نتوانیم آنرا بصورت کسری بنویسیم که صورت و مخرج آن عضوی از اعداد صحیح نباشد و مخرج هیچگاه صفر نباشد را عدد گنگ مینامیم. یا به عبارت دیگر عددی که عدد گویا نباشد عدد گنگ است.
نکته: رقم های اعشاری یک عدد گنگ، بی پایان و بدون تکرار است.
نکته: مجموعه اعداد گویا و اعداد گنگ هیچگونه اشتراکی با هم ندارند.
نکته: عدد π یک عدد گنگ است، یعنی عددی است که رقم های اعشاری آن بی پایان و بدون تکرار است.
نکته: اجتماع عدد های گویا و عدد های اصم یا گنگ، مجموعه عددهای حقیقی را تشکیل میدهد. ( میتوانید نمودار ون اعداد حقیقی را در تصویر زیر مشاهده کنید. )
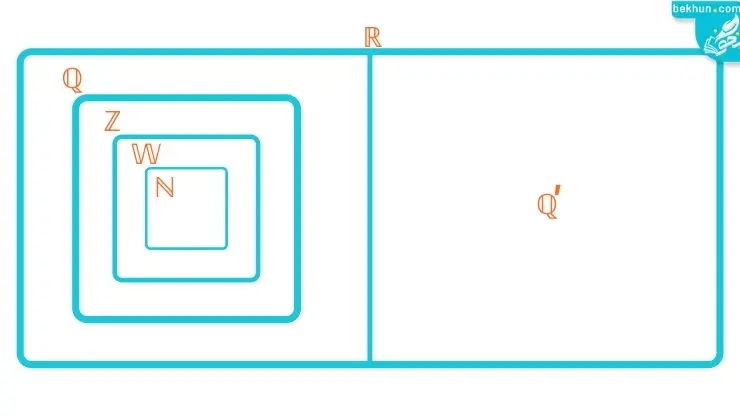
کلاس نهمیهای بخون، اگر برای انتخاب رشته خود سردرگم هستید، و سوالات زیادی در این مورد دارید. با 10 دقیقه مطالعه مشاوره انتخاب رشته نهم به دهم، میتوانید به راحتی در مورد آینده تحصیلی خود تصمیم بگیرید.
نمایش اعداد گنگ روی محور
اگر اعداد گویای بین دو عدد صحیح 0 و 1 را بخواهیم روی محور نشان دهیم، و هر نقطه را که معرف یک عدد گویا باشد را رنگ آمیری کنیم، همه نقاط بین 0 و 1 بطور یکنواخت رنگ نمیشود بلکه حفرههایی به وجود میآید که جایگاه اعداد گنگ است. پس متناظر با با هر عدد گنگ، یک نقطه روی محور وجود دارد. حال اگر بخواهیم شیوه نمایش این اعداد را بیان کنیم، باید طبق مثال زیر عمل کنیم.
مثال: نقطه نمایش عدد گنگ رادیکال 3 را روی محور نشان دهید.
پاسخ: پاسخ را میتوانید در تصویر زیر مشاهده کنید.
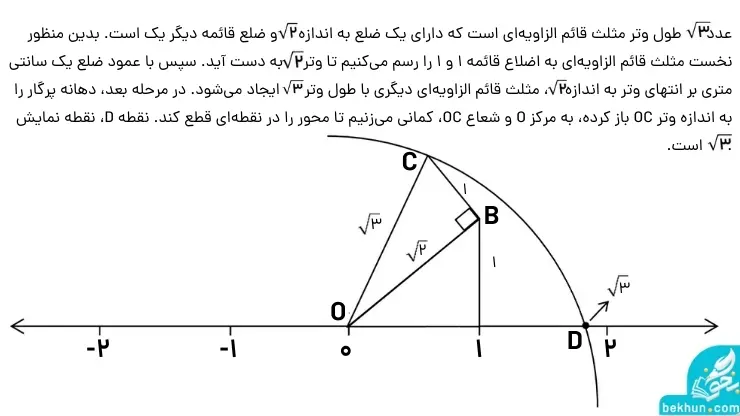
اعداد حقیقی فصل دوم ریاضی نهم
اعداد گنگ و اعداد گویا دو مجموعه جدا از هم را تشکیل میدهند، یعنی هیچگونه اشتراکی با یکدیگر ندارند. اجتماع این دو مجموعه، مجموعه بزگتری را میسازد که مجموعه اعداد حقیقی نامیده میشود و آن را با نماد R نمایش میدهیم. پس داریم:
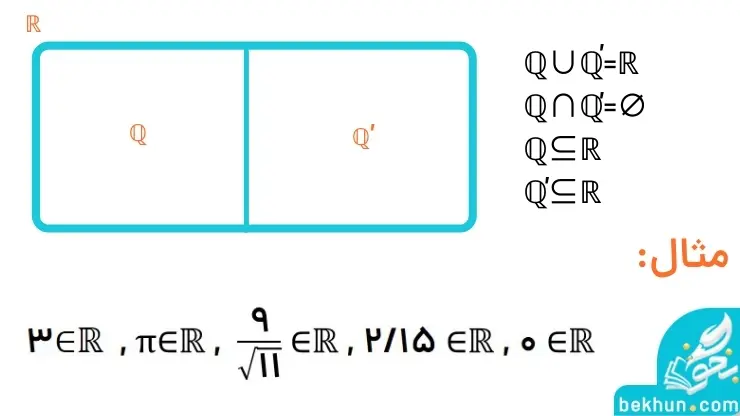
همچنین برای رسیدن به پاسخ قسمتهای مختلف فارسی نهم بر روی عناوین زیر کلیک کنید:
قدر مطلق چیست؟ ریاضی نهم
دو نقطه A و B را روی محور زیر در نظر بگیرید:
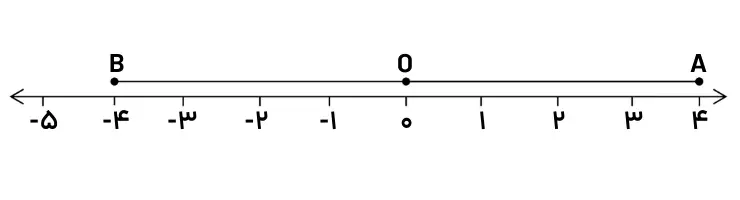
فاصله هر کدام از نقطههای A و B تا نقطه O برابر 4 میباشد یعنی اندازه پاره خطهای OA و OB برابر 4 است. میدانیم که فاصله، همیشه مقداری مثبت است پس نقطه چه در طرف مثبتها باشد و چه در طرف منفیها، فاصله آن تا مبدا ( نقطه O ) مقداری مثبت است. فاصله نقطه نمایش عدد a مینامند و با علامت | a | ( قدر مطلق a ) نمایش میدهند. پس در مثال بالا داریم:
- OB=|-4|=4
- OA=|4|=4
مثال: به محاسبات زیر دقت کنید.

نکته: قدر مطلق حاصل ضرب دو عدد، مساوی با حاصل ضرب قدر مطلق آنهاست، یعنی اگر a و b دو عدد حقیقی باشند، خواهیم داشت: |a b|=|a| |b|
نکته: قدر مطلق مجموع دو عدد، از مجموع قدر قدر مطلق های آن دو عدد، کوچکتر یا مساوی با آن است. به عبارت دیگر اگر a و b دو عدد حقیقی باشند، آنگاه خواهیم داشت: |a+b|≤|a|+|b|
نکته: برای راحتی در محاسبه عبارتهای دارای قدر مطلق، بهتر است مقدار تقریبی هر یک از از عددهای تصویر زیر را به خاطر بسپارید.
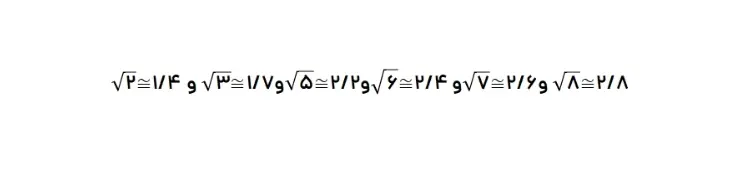
با توجه به نکاتی که در بالا ذکر شد، محسابات تصویر زیر را انجام میدهیم.
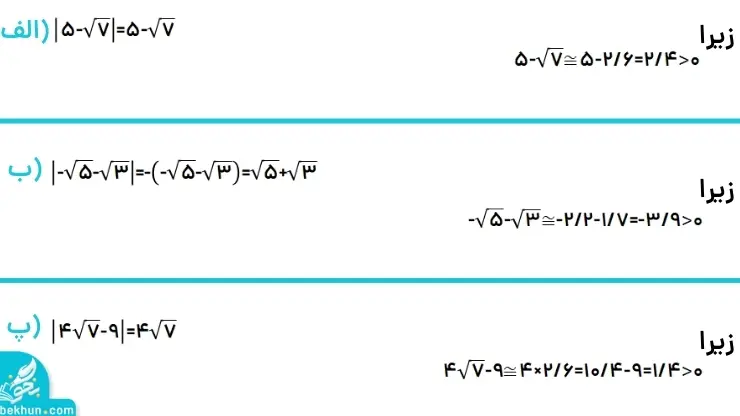
دوستان عزیز،این مقاله کامل ترین آموزش فصل دوم ریاضی نهم می باشد که می توانید با آن نمره کامل را کسب کنید و مثال های خوبی را یاد بگیرید. در ضمن برای نمونه سوالات امتحانی هم دیگر نیازی نیست که نگران باشید؛ در بخش نمونه سوال ریاضی نهم برای تمامی فصل ها یک بانک سوال رایگان را برای شما آماده کرده ایم و کافیست از طریق لینک قبلی وارد شوید. منتظر نظرات، سوالات، انتقادات و پیشنهاد شما در این مقاله از طریق بخش نظرات هستیم. از طریق عناوین زیر هم میتوانید به کل مطالب مربوط به هردسته به صورت کاملا رایگان دسترسی داشته باشید:
سوالات متداول
- آیا در مقاله آموزش فصل دوم ریاضی نهم، مطابق با کتاب های درسی جدید این آموزش آماده شده است؟
بله! براساس آخرین تغیرات کتاب های درسی آموزش ها تدوین شده اند. - فصل دوم ریاضی نهم شامل کدام مباحث است؟
اعداد حقیقی، اعداد گویا و قدر مطلق و کاربرد آن - فصل دوم ریاضی نهم با کدام یک از فصل ها در سایر پایه ها مرتبط است؟
با فصل اول ریاضی هشتم و فصل دوم ریاضی هفتم






