سلامی دوباره به خوانندگان عزیز این مقاله، حتما آموزش فصل اول ریاضی نهم را به خوبی مطالعه کرده اید که سراغ جواب به سوالات آن آمدهاید. ما سعی کردیم به سوالات به سادهترین و بهترین روش ممکن پاسخ دهیم، تا شما عزیزان هم وقت کمتری صرف کنید هم زودتر و بهتر یاد بگیرید. اصلا نگران نباشید، سوالات این فصل به ظاهر طولانی و سخت میباشند؛ اما شما میتوانید در عرض 10 دقیقه همگی سوالات را یاد بگیرید و به راحتی به آنها پاسخ دهید.
من ناصر گاگمی هستم و امروز می خواهیم با هم،در گام به گام فصل اول ریاضی نهم، پاسخ تمامی فعالیتها، کار در کلاسها و تمرینات را بطور کامل بدهیم. سوالات را به صورت عکس میتوانید مشاهده کنید و پاسخها را بصورت تشریحی و کوتاه در پایین عکسها قرار دادهایم.
خلاصه فصل اول ریاضی نهم
فصل اول ریاضی نهم با عنوان مجموعهها نامگذاری شده است، که شامل مباحث زیر میباشد:
- معرفی مجموعهها
- عضویت در مجموعهها
- نمایش مجموعهها
- اجتماع، اشتراک و تفاضل مجموعهها
- مجموعهها و احتمال
حالا که مباحث اصلی درس اول ریاضی نهم را یادآوری کردیم، به سراغ جوابهای فصل اول ریاضی نهم میرویم.
جواب فعالیت صفحه 2 ریاضی نهم

سوال: مجموعه D شامل همه شمارندههای دو رقمی 60 را تشکیل دهید؛ این مجموعه چند عضو دارد؟
پاسخ: D={10،12،15،20،30،60}
سوال: از رضا و احمد خواسته شد تا مجموعهی شامل 3 شمارنده زوج عدد 60 را تشکیل دهند. احمد نوشت: { 10،6،4} و رضا نوشت: {12،10،6} به نظر شما چرا جوابهای آنها با هم فرق دارد؟
پاسخ: چون کاملا مشخص نشده است منظور کدام عددهای زوج است.
دوستان عزیز کلاس نهمی، پس از اینکه سوالات فصل اول را به پایان رساندید، به شما پیشنهاد میکنم مقالهی گام به گام فصل دوم ریاضی نهم | عددهای حقیقی را نیز به خوبی مطالعه کنید، تا فصل اول و دوم ریاضی نهم خود را به خوبی یاد بگیرید.
جواب فعالیت صفحه 3 ریاضی نهم

پاسخ 1:
- الف: A={1،2،3،4،5،6،7،8،9}
- ب: نمیتوان یک مجموعه را مشخص کرد، چون نمیدانیم کدام چهار شاعر مد نظر است، یعنی عضوهای مجموعه کاملا مشخص نیست. ( در این قسمت عضوهای مجموعه مشخص نیستند. )
- ج: نمیتوان یک مجموعه را مشخص کرد، چون معلوم نیست، کدام دو عدد اول کوچکتر از 12 درون این مجموعه قرار دارند. یعنی عضوهای مجموعه کاملا مشخص نیست.
پاسخ 2:
- الف: به جای A={1،2،1،4،5} باید بنویسیم A={1،2،4،5}
- ب: به دلیل تکراری بودن عدد 5 در B={5،6،5،7} آن را بصورت B={5،6،7} مینویسیم.
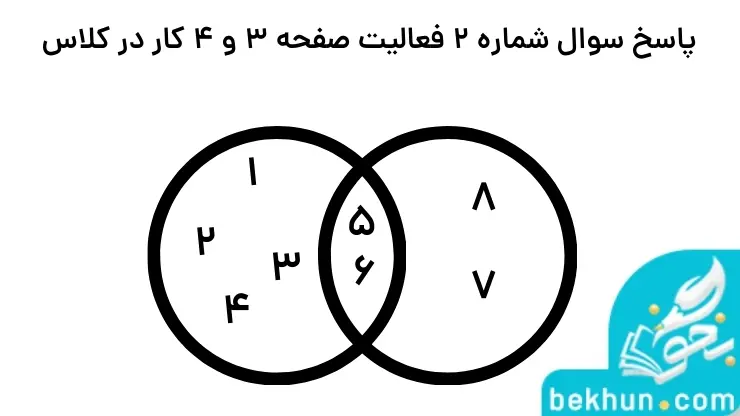
جواب فعالیت صفحه 3 و 4 ریاضی نهم

پاسخ 1: A={a، b، c، s، f، k} و B={s، f، k، m، n}
پاسخ 2: اعداد 5 و 6 هم در منحنی بسته مربوط به A و هم در منحنی بسته B وجود دارند.
کلاس نهمی های بخون، اگر در پیدا کرن پاسخ آزمایش کنیدهای کتاب علوم خود دچار مشکل شدهاید، اصلا لازم نیست که نگران باشید ما برای شما در مقالهی جواب آزمایش کنیدهای علوم نهم پاسخ تمامی آزمایش کنیدهای علوم نهم را بطور کامل قرار دادهایم.
پاسخ 3: از آنجا که هر عدد زوج دو رقمی، به جز 1 و خودش بر عدد 2 بخشپذیر است پس، هیچکدام از عددهای زوج دو رقمی اول نیستند. بنابراین مجموعه E هیچ عضوی ندارد.
پاسخ 4
- الف: این عبارت مجموعه تهی را مشخص میکند.
- ب: این مجموعه شامل عضو صفر میباشد، پس تهی نیست.
- ج: این مجموعه شامل عدد 2 است، پس تهی نیست.
- د: این مجموعه شامل عدد 3 است، پس تهی نیست.
جواب کار در کلاس صفحه 4 و 5 ریاضی نهم

پاسخ 1: (اعداد طبیعی کوچکتر از 1) و (اعداد صحیح بین منفی 6 و منفی 7) و ( اعداد طبیعی زوج بین 2 و 4)
پاسخ 2:( مجموعه عددهای طبیعی بین صفر و 2) و ( مجموعه جوابهای معادله x+1=3) و ( مجموعه حروف غیر عربی کلمه “تگرگ”)
پاسخ 3
- الف: غلط، یک مجموعه را مشخص نمیکند، چون عضوهای آن کاملا مشخص نیستند.
- ب: صحیح، {6،4،2}
- ج: صحیح، {19،17،13،11،7،5،3،2}
- د: غلط، یک مجموعه را مشخص نمیکند، چون عضوهای آن کاملا مشخص نیستند.
- ه: صحیح، {24،12،8،6،4،3،2،1}
- و: غلط، یک مجموعه را مشخص نمیکند، چون عضوهای آن کاملا مشخص نیستند.
- ز: صحیح، در واقع مجموعه تهی را مشخص میکند.
پاسخ 4: پاسخ سوال 4 بصورت عکس زیر میباشد.

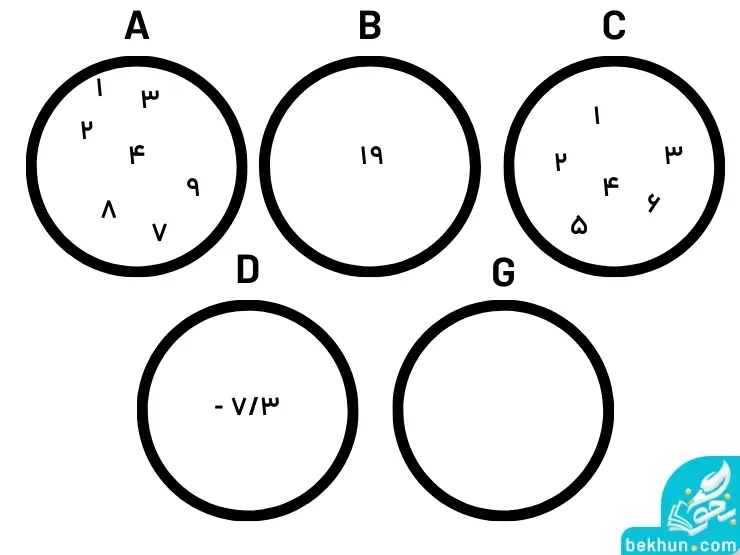
پاسخ 5
- الف: A={1،2،3،4،5،6،7،8،9}
- ب: B={19}
- ج: C={1،2،3،4،5،6}
- د: D={-7/3}
- ه: این عبارت یک مجموعه را مشخص نمیکند، چون عضوهای آن کاملا مشخص نیست.
- و: G=Ø
نمودار ونهای مربوط به سوالات بالا در عکس زیر قابل مشاهده است:
فارسی نهم، یکی یگر از دروس مهم پایه نهم به شمار میآید. شما با مطالعه مقالهی جواب نوشتنهای فارسی نهم، میتوانید پاسخ تمامی نوشتنهای فارسی نهم را به صورت یکجا و رایگان در اختیار داشته باشید.
جواب تمرین ریاضی نهم صفحه 5

پاسخ 1:
- الف: مجموعه عددهای طبیعی مکعب کامل کوچکتر از 130
- ب: مجموعه کوچکترین عدد طبیعی دو روقمی
- ج: A={5،10،15،20،…،95}
- د: مجموعه تهی
- ه: مجموعه تهی
- د: مجموعه تهی
پاسخ 2:
- الف: عبارت 5 عدد طبیعی که بین 1 و 20 قرار داشته باشد یک مجموعه را مشخص نمیکند.
- ب: مجموعه {9 … 4 3 2} دارای 8 عضو است.
- ج: مجموعه {Ø، 0}=A دارای 2 عضو است.
- د: با توجه به مجموعه A={3،5،7،9،11}: داریم 5 عضو A است یا با نماد ریاضی A∋5 و 12 عضو A نیست یا با نماد ریاضی 12∉A.
پاسخ 3:
- مجموعه عددهای طبیعی = {…، 4،3،2،1}
- مجموعه عددهای طبیعی زوج = {…، 8،6،4،2}
- مجموعه عددهای اول یک رقمی = {7،5،3،2}
جواب کار در کلاس صفحه 6 ریاضی نهم

پاسخ سوال یک و دو به صورت عکس زیر میباشد.

جواب کار در کلاس صفحه 8 ریاضی نهم

پاسخ 1:
- A⊄C، نادرست است. زیرا تمام عضوهای A حتما در مجموعه C نیز وجود دارند.
- B⊆A، نادرست است. زیرا طبق شکل B عضوهایی دارد که در A نیستند.
- C⊄A، درست است. زیرا C به جز عضوهای A، عضوهای دیگری نیز دارد.
- Ø⊆A، درست است زیرا Ø هیچ عضوی ندارد که در A وجود نداشته باشد.
- B⊆C، درست است. زیرا همه عضوهای B حتما درون C نیز موجودند.
- A⊆B، درست است. زیرا هر عضو A حتما عضوی از B نیز هست.
پاسخ 2:
- B⊄A، درست است. زیرا عدد 5 در B هست ولی در A نیست.
- 3⊆B، نادرست است. زیرا عدد 3 در یک مجموعه نیست.
- A⊆B، نادرست است. زیرا عددهای 4 و 6 در B نیستند در حالی که در A وجود دارند.
- B⊆C، درست است. زیرا هر سه عدد 3 و 1 و 5 در C نیز موجودند.
- A⊄C، درست است. زیرا عدد 4 عضو A است ولی در C نیست.
- 2⊆A، نادرست است. زیرا عدد 2 در مجموعه A وجود ندارد.
- {1 4}⊆A، نادرست است. زیرا 4 و 1 در A وجود ندارند.
- 6⊄A، نادرست است. زیرا عدد 6 درون A موجود است.
- {6 5}⊆C، درست است. زیرا هر دو عدد 6 و 5 در C موجود هستند.
- 5⊆C، درست است. زیرا عدد 5 عضو مجموعه C است.
- 0⊆A، نادرست است.
پاسخ 3
- الف: {11،10}
- ب: {a، b، c، d}
نهمیهای عزیز، اگر در حل کردن سوالات درس یک زبان خود دچار مشکل شدهاید، پس عجله کنید و زود مقالهی گام به گام درس اول زبان نهم | Personality را مطالعه کنید.
جواب کار در کلاس صفحه 10 ریاضی نهم

پاسخ الف: {…، 5،3،1،1-، 3-، 5-، …}
پاسخ ب: {4، …، 4-، 5-}=A
پاسخ ج: {…، 5،2،1-، 4-، …}=B
حل تمرین صفحه 10 ریاضی نهم

پاسخ 1: B={-1،0،1} و C={-1،0،1} و D={-1،1} پس دو مجموعه B و C باهم برابرند.
پاسخ 2: A={1،2،3} و B={1،2،3،4} و C={1،2،3،4،5}. بله با توجه به سه مجموعه A و B و C میتوان نتیجه گرفت هرگاه A⊆B و B⊆C، آنگاه حتما A⊆C.
پاسخ 3
- الف: 2x+1=3⇒2x=3-1⇒x=1⇒A{1}
- ب: B={0،4،6}
پاسخ 4: N⊆W⊆Z⊆Q
پاسخ 5
- الف: نادرست است. زیرا 1/2 عددی گویاست که در مجموعه عددهای حسابی نیست.
- ب: درست است. زیرا هر عدد حسابی a به صورت a/1 قابل نوشتن است، پس گویا نیز هست.
- ج: درست است. زیرا هر عدد حسابی a به صورت a/1 قابل نوشتن است، پس گویا نیز هست.
- د: درست است. عددهای گویایی که در آنها صورت بر مخرج بخشپذیر باشد، عدد صحیح است.
جواب فعالیت صفحه 11 ریاضی نهم

پاسخ 1
- الف: { رضا و علی و فرشید و سامان و حسین و احسان}=V و { رضا و علی و محمد و سبحان و حسن و کیوان}=F
- ب: {رضا و علی}
- ج: { محمد و کیوان و حسن و سبحان و حسین و احسان و فرشید و سامان و رضا و علی}
پاسخ 2
- الف: {6 5 4 3 2 1}=A
- ب: {3 2 1 0 1- 2-}=B
- ج: مجموعه عددهایی که در هر دو مجموعه A و B هست= {3،2،1}
- د: مجموعه عددهای که حداقل در یکی از دو مجموعه A و B هست. = {6 5 4 3 2 1 0 1- 2-}
ما برای شما نهمیها، یک مقالهی جامع از پیامهای آسمانی تهیه کردهایم. ما در مقالهی جواب فعالیت کلاسی پیامهای آسمانی نهم، پاسخ تمامی فعالیتهای کلاسی پیام های نهم را بصورت یکجا و کامل قرار دادهایم.
جواب فعالیت صفحه 12 ریاضی نهم
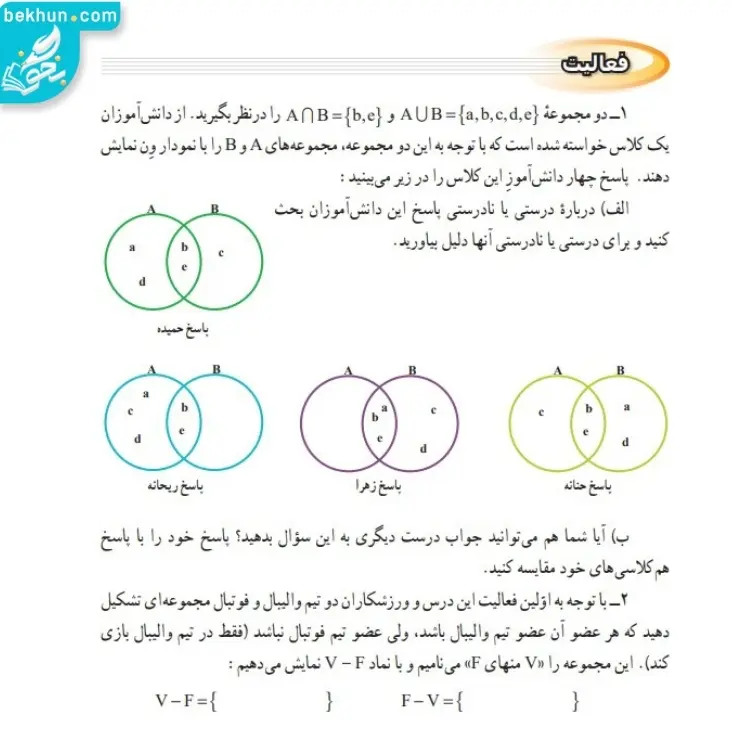
پاسخ 1-الف:
- پاسخ حمیده درست است. زیرا طبق نمودار ون b و e به هر دو مجموعه A و B تعلق دارند و همچنین عضوهایی که حداقل عضو یکی از دو مجموعه A یا B باشند عبارتند از a و b و c و d و e.
- پاسخ ریحانه درست است. زیرا اولا b و e عضو هر دو مجموعه A و B هستند. ثانیا عضوهایی که حداقل به یکی از دو مجموعه A یا B متعلق باشند a و b و C و d و e است.
- پاسخ زهرا نادرست است. زیرا مجموعه عضوهایی که به هر دو مجموعه A و B تعلق دارند عبارت است از {a، b، e}، بنابراین A∩B={a، b، e} است که با خواسته مسئله متفاوت است.
- پاسخ حنانه درست است. زیرا b و e عضوهایی هستند که هم به A و هم به B متعلقاند. ثانیا عضوهایی که حداقل به یکی از دو مجموعه A یا B تعلق داشته باشند عبارتند از a و b و c و d و e.
پاسخ 1-ب: بله، با مقایسه پاسخ خود و دیگر همکلاسیها مشاهده میکنیم که تعداد حالتهایی که بتوان A و B را طبق شرایط داده شده تشکیل داد، متنوع است و یک جواب واحد بدست نمیآید.
پاسخ 2: { حسین و فرشید و سامان و احسان}=V-F و { محمد و کیوان و حسن و سبحان}=F-V
جواب کار در کلاس صفحه 13 ریاضی نهم
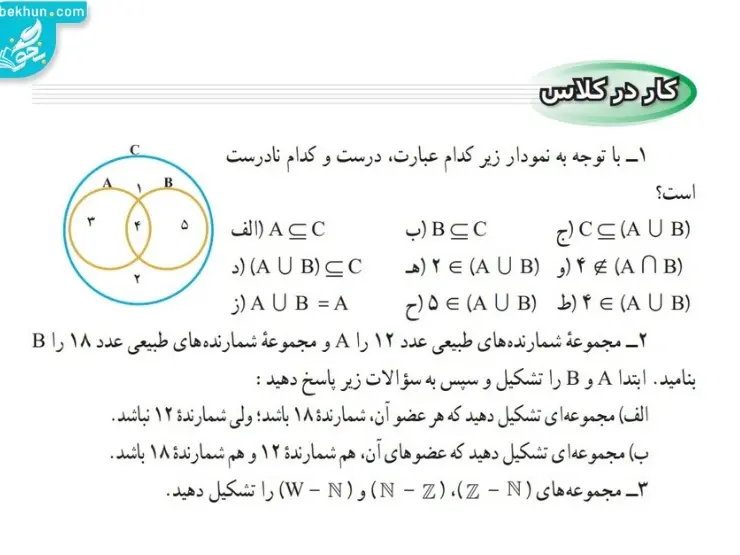
پاسخ 1:
- الف:درست
- ب:درست
- ج:نادرست
- د:درست
- ه:نادرست
- و:نادرست
- ز:نادرست
- ح:درست
- ط:درست
پاسخ 2:
- A={1، 2، 3، 4، 6، 12} و B={1، 2، 3، 6، 9، 18}
- الف: B-A={9، 18}
- ب: A∩B={1، 2، 3، 4}
پاسخ 3: Z-N={0، -1، -2، -3 …} و N-Z=Ø و W-N={0}
جواب تمرین صفحه 14 ریاضی نهم
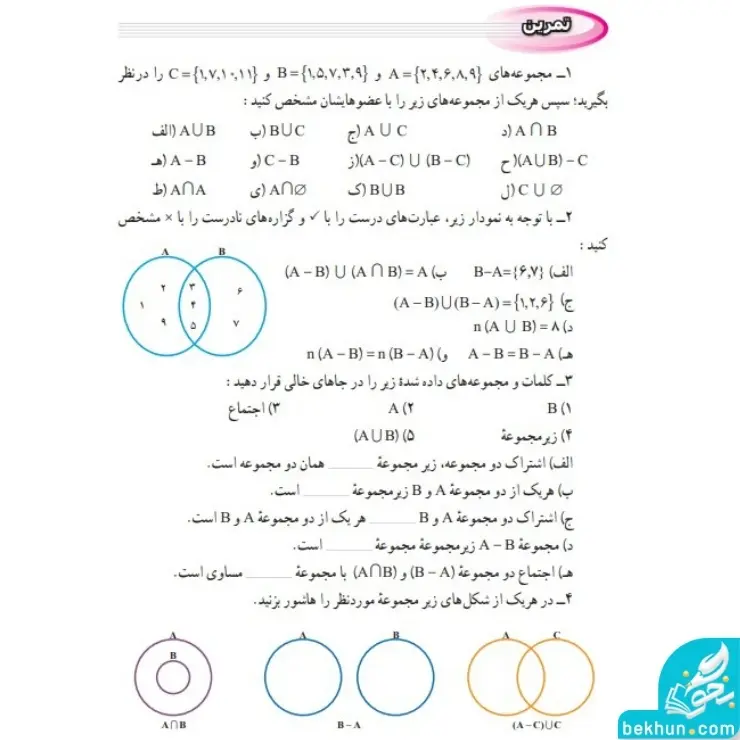
پاسخ 1:
- الف: { 9،8،7،6،5،4،3،2،1}
- ب: {11،10،9،8،7،5،3،1}
- ج: {11،10،9،8،7،6،4،2،1}
- د: {9}
- ه: {8،6،4،2}
- و: {11،10،8}
- ز: {9،6،5،4،3،2}
- ح: {9،6،5،4،3،2}
- ط: {9،8،6،4،2}
- ی: Ø
- ک: {9،3،7،5،1}
- ل: {11،10،8،7،1}
پاسخ 2:
- الف: درست
- ب: درست
- ج: نادرست
- د: درست
- ه: نادرست
- و: نادرست
پاسخ 3:
- الف: اشتراک دو مجموعه، زیر مجموعهی اجتماع همان دو مجموعه است.
- ب: هر یک از دو مجموعه A و B زیر مجموعه A∪B میباشند.
- ج: اشتراک دو مجموعه A و B زیر مجموعه هر یک از دو مجموعه A و B است.
- د: مجموعهی A-B زیر مجموعه، مجموعه A است.
- ه: اجتماع دو مجموعه B-A و A∩B مساوی با مجموعه B است.
پاسخ 4: پاسخ سوال 4 بصورت عکس زیر میباشد.
 جواب کار در کلاس صفحه 16 ریاضی نهم
جواب کار در کلاس صفحه 16 ریاضی نهم

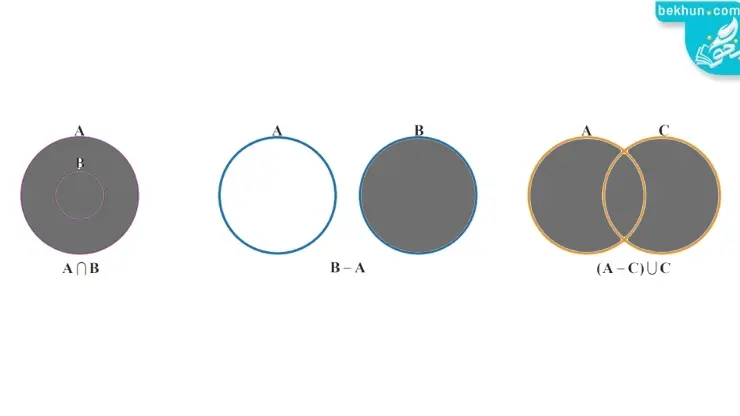
پاسخ الف: پاسخ سوال الف بصورت زیر میباشد.
پاسخ ب: پاسخ سوال ب بصورت زیر میباشد.
اما یک مقالهی ویژه در اینجا برای شما نهمیها در نظر گرفتهایم. شما با مطالعه مقالهی جواب فعالیت های مطالعات اجتماعی نهم به راحتی میتوانید در امتحان خود نمره 20 را کسب کنید.
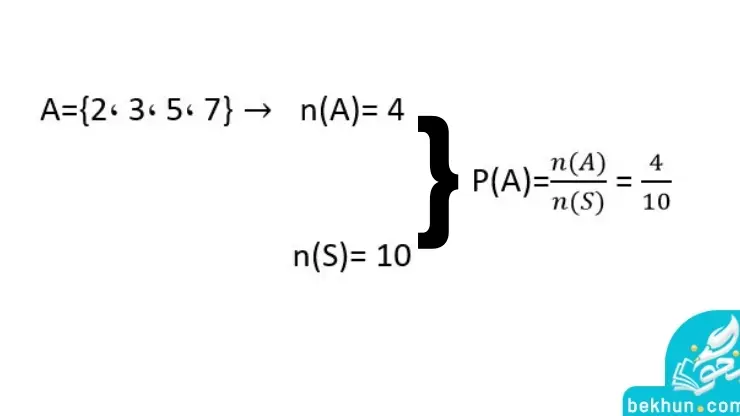
پاسخ ج: پاسخ سوال ج بصورت زیر میباشد.
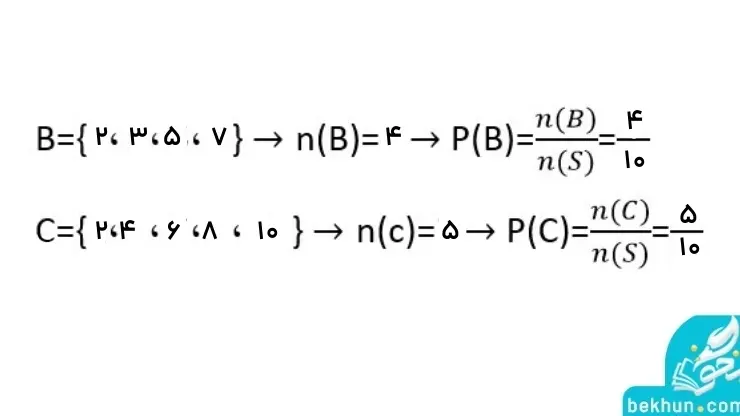
جواب تمرین صفحه 17 ریاضی نهم

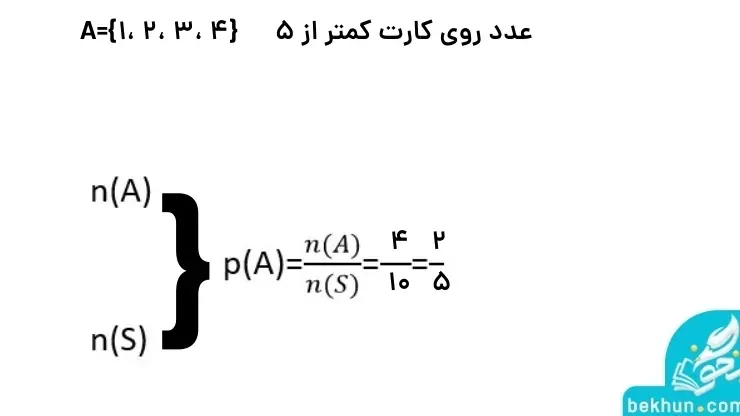
پاسخ 1: وقتی تاسی را میاندازیم شش حالت ممکن است اتفاق بیافتد که عبارتند از 1 و 2 و 3 و 4 و 5 و 6 بنابراین: S={1،2،3،4،5،6} و n(S)=6. ادامه پاسخ را در عکس زیر میتوانید مشاهده کنید.
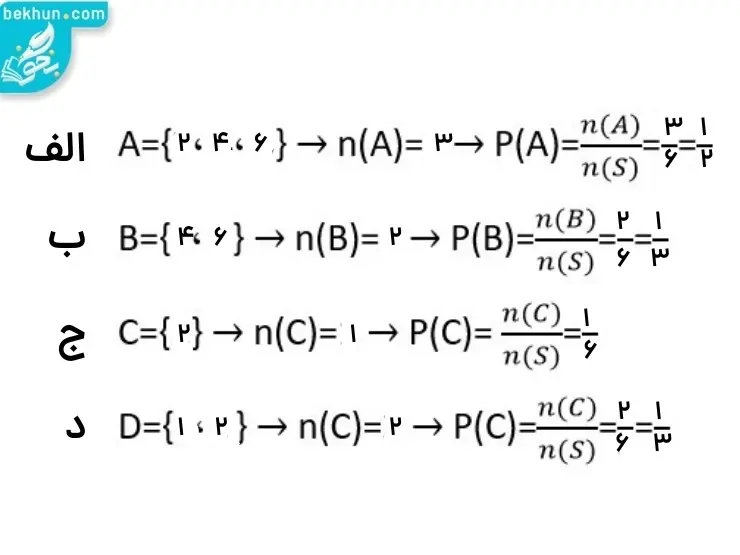
پاسخ 2: پاسخ سوال شماره 2 را میتوانید در تصویر زیر مشاهده کنید.
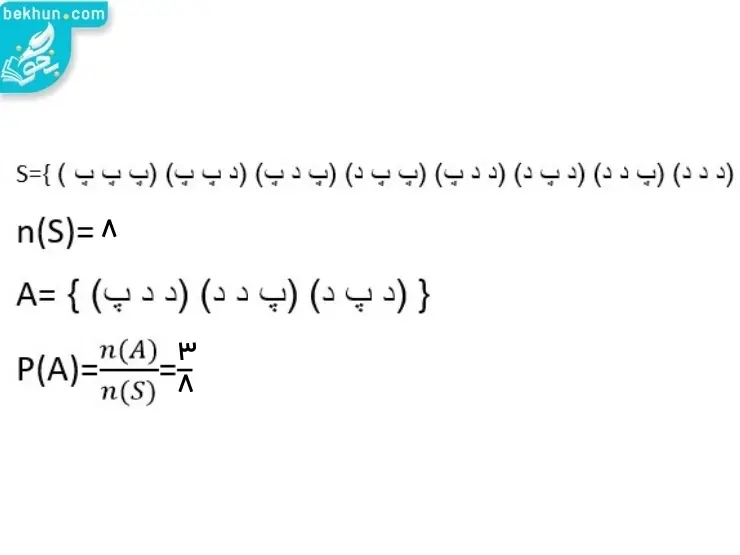
پاسخ 3: پاسخ سوال شماره 3 را میتوانید در تصویر زیر مشاهده کنید.
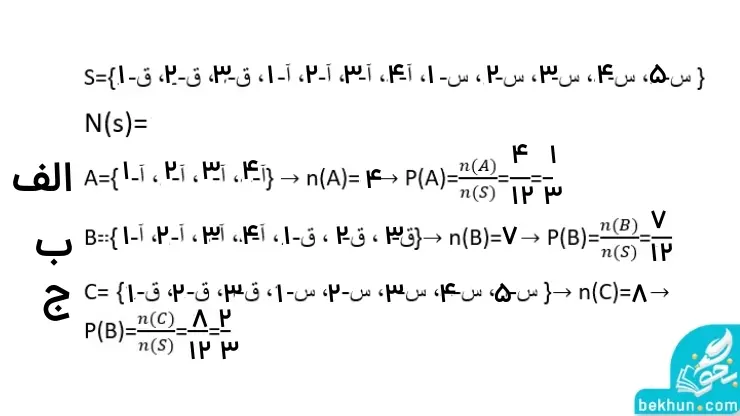
پاسخ 4: پاسخ سوال شماره 4 را میتوانید در تصویر زیر مشاهده کنید.
اگر هنوز نتوانستهاید پاسخ فعالیتهای قرآن نهم خود را پیدا کنید، ما برای شما پاسخ تمامی فعالیتهای قرآن نهم را در لینک جواب فعالیت قرآن نهم قرار دادهایم.

دوستان عزیز به پایان سوالات رسیدیم، سعی کردیم پاسخ همه سوالات را به درستی و تکمیلی برای شما دوستان در این مقاله قرار دهیم. حتما فهمیدید که واقعا سوالات آسانی بودند و توانستید بر آنها کاملا مسلط شوید. امیدوارم که این پاسخها برای شما مفید واقع شده باشد. باعث خوشحالی ما میشوید اگر نظرات خود را برای ما بفرستید. همچنین میتوانید نمونه سوالات بیشتری را در مقاله نمونه سوالات فصل اول ریاضی نهم داشته باشید. دوستان عزیز با کلیک بر روی عناوین زیر نیز، میتوانید به سایر مباحث پایه نهم دسترسی داشته باشید:
سوالات متداول
- آیا در مقاله گام به گام فصل اول ریاضی نهم، پاسخ تمامی سوال قرار داده شده است؟
بله، پاسخ همه فعالیتها، کار در کلاسها و تمرینها بطور کامل در این مقاله قرار داده شده است. - آیا آموزش فصل اول ریاضی نهم همراه با نمونه سوالات هم در سایت قرار دارد؟
بله، شما میتوانید با مراجعه به سایت بخون به همه آموزشها و نمونه سوالات بالا دسترسی داشته باشید. - فصل اول ریاضی نهم، شامل چه مباحثی میباشد؟
معرفی مجموعهها، عضویت در مجموعهها، نمایش مجموعهها، اجتماع، اشتراک و تفاضل مجموعهها، مجموعهها و احتمال

 جواب کار در کلاس صفحه 16 ریاضی نهم
جواب کار در کلاس صفحه 16 ریاضی نهم




