آموزش فصل اول ریاضی نهم | مجموعه ها

در فصل هشتم ریاضی پایه هشتم تا حدودی با مفاهیم مربوط به احتمال آشنا شدید که در فصل اول ریاضی نهم به صورت گسترده‌‌تر مفاهیم مربوط به آن را یاد خواهید گرفت. من ناصر گاگمی هستم و امروز در سایت بخون با آموزش فصل اول ریاضی نهم در خدمت شما عزیزان هستم. در فصل اول ریاضی نهم در کتاب درسی ما 4 درس روبرو خواهیم شد که به صورت زیر می‌باشد:

• معرفی مجموعه
• مجموعه های برابر و نمایش مجموعه ها
• اجتماع، اشتراک و تفاضل مجموعه ها
• مجموعه ها و احتمال

شاید در نگاه اول کمی مفاهیم این فصل ترسناک باشد، اما اصلا نگران نباشید، در این مقاله اعجاب انگیز به صورت کامل آموزش فصل اول ریاضی نهم را در اختیارتان قرار خواهم داد و اگر با صبر این مطلب را تا انتها بخوانید، به راحتی می‌توانید مفاهیم این فصل را یاد بگیرید. در ضمن اگر برای سایر فصل های ریاضی نهم هم به دنبال یک آموزش کامل و رایگان هستید حتما لینک مربوط به آموزش ریاضی نهم را یک‌جا ذخیره کنید، چون مطمئنا جایی به دردتان خواهد خورد.

آموزش فصل اول ریاضی نهم | مجموعه‌ها

درس اول ریاضی نهم، یکی از آسان‌ترین و ساده‌ترین فصل‌های این کتاب است. شما با یادگیری مباحث مجموعه و اشتراک و اجتماع و همچنین تفاضل آن‌ها کاملا می‌توانید به مباحث این فصل تسلط داشته باشید. همچنین می توانید تمامی پاسخ های سوالات این فصل را در مقاله، گام به گام فصل اول ریاضی نهم داشته باشید.

معرفی مجموعه‌ها و انواع آن، ریاضی نهم

ابتدا برای یادگیری بهتر مجموعه و تعریف آن چند تعریف دیگر را به کار می‌بریم تا از آن‌ها در مثال‌ها و سایر آموزش‌ها استفاده کنیم.

• تعریف عدد اول: عدد طبیعی بزرگتر از یک که فقط، بر خودش و یک بخش پذیز است. مانند اعدادی چون 2،3،5 و …. همچنین این نکته را به یاد داشته باشید که تنها عدد زوج اول، عدد 2 است.
• 
• تعریف عدد مرکب: هر عددی که به صورت حاصل ضرب دو عدد بزرگتر از یک باشد عدد مرکب است. مانند اعدادی چون 12،6،8 و ….
• تعریف شمارنده: همه اعدادی که یک عدد بر آن‌ها بخش‌پذیر است، شمارنده‌های آن عدد هستند. برای مثال عدد 24 که شمارنده‌های آن 1،2،3،4،6،8،12 و 24 هستند.
• تعریف مضارب طبیعی یک عدد: همه عدد‌هایی که از ضرب یک عدد، در اعداد طبیعی بدست می‌آید مضارب طبیعی آن عدد هستند.

تعریف مجموعه

به هر دسته از اشیاء مشخص و متمایز ( غیر تکراری) یک مجموعه می‌گویند، و آن اشیاء را عضو آن مجموعه می‌نامند. همچنین جمله‌ای که اعضای یک مجموعه را مشخص می‌کند، باید کاملا واضح و درست باشد.

مثال 1: کدام یک از دسته‌های زیر یک مجموعه را به درستی مشخص می‌کند؟

1. اعداد طبیعی بزرگتر از 1000
2. اعداد خیلی بزرگ
3. چهار عدد فرد متوالی شروع از 3
4. مقسوم علیه‌های عدد 30

پاسخ: هر یک از گزینه‌های بالا، اعضای مشخصی دارند به جز گزینه 2 که اعضای آن کاملا مشخص نیستند. پس همه گزینه‌ها به جز گزینه شماره 2 یک مجموعه به شمار می‌آیند.

دوستان خوبم به شما پیشنهاد می‌کنم، پس از اینکه این آموزش را به خوبی پشت سر گذارندید، با کلیک بر روی لینک گام به گام فصل اول ریاضی نهم | مجموعه‌ها پاسخ تمامی سوالات فصل یک ریاضی نهم را نیز به خوبی مطالعه کنید.

نکات مجموعه‌ها، آموزش درس اول ریاضی نهم

نکات زیر را در مورد تمامی مجموعه‌ها به یاد داشته باشید.

• برای نام‌گذاری مجموعه‌ها از حروف بزرگ انگلیسی استفاده می‌شود.
• جابه جایی اعضای مجموعه، مجموعه را تغییر نمی‌دهد.
• در نمایش مجموعه‌ها ترتیب نوشتن اعضا اهمیتی ندارد.
• اعضای هر مجموعه را با (و) یا ویرگول (، ) از هم جدا می‌کنند.

مثال 2: مجموعه A={a، b، a، b، c} چند عضو دارد؟

پاسخ: این مجموعه سه عضو دارد یعنی a و b و c.

عضویت در مجموعه‌ها

اگر x عضو مجوعه A باشد، می‌نویسیم x∈A. در این صورت باید x عینا در مجموعه A دیده شود. و اگر y عضو A نباشد باید بنویسیم y∉A.

نمایش مجموعه‌ها با استفاده از نمودار ون

مجموعه‌ها را می‌توان با استفاده از منحنی‌ها یا خط‌های شکسته بسته نمایش داد.

مثال 3: مجموعه A={2،3،4} را به صورت نمودار ون نمایش دهید.

پاسخ: پاسخ در تصویر زیر نمایش داده شده است.

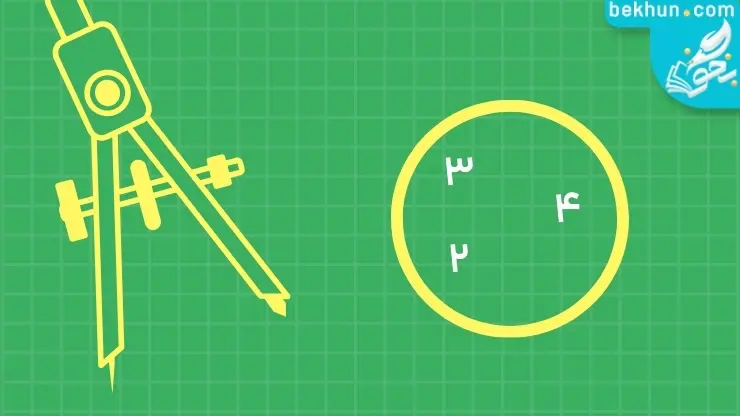
مجموعه تهی

مجموعه‌ای که هیچ عضوی نداشته باشد، مجموعه تهی نام دارد و با علامت Ø نمایش داده می‌شود.

مثال 4: کدام یک از مجموعه‌های زیر تهی است؟

1. اعداد اول طبیعی بین 1 و 2
2. اعداد اول یک رقمی

پاسخ: در گزینه 1 هیچ عضوی وجود ندارد، پس گزینه یک پاسخ درست است.

کلاس نهمی‌های عزیز، همه ما می‌دانیم که امتحانات شما امسال بصورت نهایی برگزار خواهد شد. پس ما سعی کرده‌ایم در مقاله جواب فعالیت‌های علوم نهم به شما در درس علوم خود کمک کرده باشیم.

درس دوم: مجموعه‌های برابر و نمایش مجموعه‌ها در ریاضی نهم

دو مجموعه A و B با هم یکسان هستند هرگاه، هر عضو A در B و هر عضو B در A باشد. به عبارت دیگر A=B باشد. هنگامی که دو مجموعه A و B نا مساوی‌اند که، حداقل یک عضو در مجموعه A باشد که در B نباشد و بالعکس.

مثال 5: جا‌های خالی را طوری پر کنید که دو مجوعه روبرو برابر باشند. {…، رادیکال 9،5}={…، 3،4}

پاسخ: چون رادیکال 9 برابر 3 می‌باشد، پس برای برابری باید عدد‌های 4 و 5 را در دو مجموعه رد و بدل کنیم. {4، رادیکال 9،5}={5،3،4}

زیر مجموعه ریاضی نهم

مجموعه B را زیر مجموعه A می‌نامیم هر گاه هر عضو مجموعه B در مجموعه A باشد، که با علامت B⊇A نشان می‌دهیم.

نکات زیر مجموعه:

• مجموعه تهی، زیر مجموعه هر مجموعه‌ی دلخواهی مانند A است. Ø⊆A
• هر مجموعه‌ای زیر مجموعه خودش است.
• اگر A⊆C و B⊆C باشد آنگاه A⊆C خواهد بود.
• تعداد زیر مجموعه‌های یک مجموعه n عضوی برابر است با: 2 به توان n

مثال6: یک مجموعه 10 عضوی چند زیر مجموعه دارد؟

پاسخ: دو به توان 10 یعنی 1024، پس 1024 زیر مجموعه دارد.

مثال 7: مجموعه همه اعداد یک رقمی را بنویسید و A بنامید، سپس مجموعه اعداد اول یک رقمی را بنویسید و B بنامید. آیا مجموعه B زیر مجموعه A است؟ چرا؟

پاسخ: A={1،2،3،4،5،6،7،8،9}، B={2،3،5،7}

چون همه اعضای B در A هستند پس B زیر مجموعه A است.

نحوه نمایش مجموعه‌ها

در کل برای نمایش مجموعه‌ها، 3 روش وجود دارد:

1. توصیفی: مجموعه را با توصیف اعضا می‌توانیم مشخص کنیم. مانند: مجموعه اعداد طبیعی کوچکتر از 10
2. بیان ریاضی: در این روش با پیدا کردن یک ویژگی مشترک و نشان دادن آن ویژگی با علائم ریاضی مجموعه را بیانی می‌کنیم. برای مثال اعداد طبیعی زوج را به صورت روبرو نمای می‌دهیم. E={2k | k∈N} به طور کلی فرمول کلی نوشتن مجموعه به صورت شکل زیر است.
3. نمودار ون که در بالا توضیح داده شده است.

درس سوم: اجتماع، اشتراک و تفاضل مجموعه‌ها

در این بخش می‌خواهیم عملیات‌هایی چون اجتماع و اشتراک را روی مجموعه‌ها اعمال کنیم. اما در همین سایت یک بخش جذاب دیگر هم برای پاسخ تمامی فعالیت ها و تمرینات کتاب درسی داریم و توصیه می‌کنیم حتما از آن از طریق بخش گام به گام ریاضی نهم اقدام کنید.

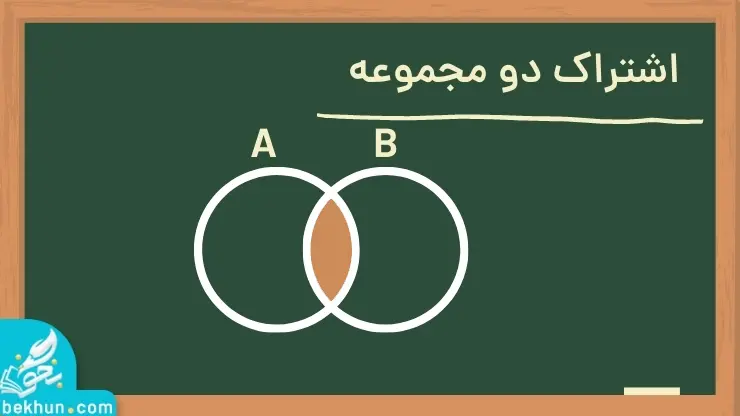
اشتراک دو مجموعه

اشتراک دو مجموعه A و B شامل همه عضو‌هایی هست که هم عضو مجموعه A و هم عضو مجموعه B هستند. این مجموعه را به صورت A∩B نشان می‌دهند. در نمودار زیر قسمت هاشور خورده، اشتراک دو مجموعه را نشان می‌دهد. A∩B={x|x∈A، x∈B}

مثال 8: دو مجموعه A={x∈W|x<3} و A={x∈N|x<5} را در نظر بگیرید A∩B را به صورت اعضا نمایش دهید.

پاسخ: {A={0،1،2 و {B={1،2،3،4 پس A∩B={1،2}

ما برای درس فارسی شما هم یک مقاله عالی در نظر گرفته‌ایم، جواب خودارزیابی‌های فارسی نهم مقاله‌ای است که در آن پاسخ تمامی خودارزیابی های فارسی نهم بطور کامل قرار داده شده است.

اجتماع دو مجموعه

اجتماع دو مجموعه A و B شامل همه‌ی عضو‌هایی هست که حداقل در یکی از دو مجموعه A و B هستند. این مجموعه را با نماد A∪B نشان می‌دهند. در نمودار زیر قسمت هاشور خورده، اجتماع دو مجموعه را نشان می‌دهد. A∪B={x|x∈A، x∈B}

مثال 9: با توجه به مجموعه‌های A={a، b، c، d} و B={c، d، f} مجموعه A∪B را نشان دهید.

پاسخ: A∪B={a، b، c، d، f}

تفاضل دو مجموعه

مجموعه A-B مجموعه است شامل همه اعضایی که عضو A باشند ولی عضو B نباشند. در شکل زیر مجموعه A-B هاشور خورده است.

مثال 10: با توجه به دو مجوعه A={1،3،5،7،9} و B={1،2،3،4،5،6} مجموعه A-B را نشان دهید

پاسخ: A-B={7،9}

عدد اصلی یک مجموعه

تعداد اعضای هر مجموعه‌ای مانند A را عدد اصلی و با n(A) نشان می‌دهند. به عنوان مثال در مجموعه D={1،2،4،7،9،11} داریم n(D)= 6.

درس چهارم: مجموعه‌ها و احتمال

مجموعه‌ی همه‌ی حالت‌های ممکن در یک پیشامد را مجموعه S می‌نامند.

نکته‌های مجموعه و احتمالات

• همه زیر مجموعه‌های S را یک پیشامد تصادفی یا مجموعه‌ی A می‌نامند.
• اگر احتمال دو پیشامد مساوی باشند آن‌ها را هم شانس گویند.
• حاصل جمع عدد‌های احتمال زیر مجموعه‌های یک پیشامد برابر 1 است.
• احتمال رخ ندادن یک احتمال از رابطه‌ی روبرو بدست می‌آید: احتمال رخداد پیشامد – عدد یک

احتمال رخداد یک پیشامد 

احتمال رخداد یک پیشامد با دستور زیر با دست می‌آید.

مثال 11: یک سکه را سه بار پرتاب می‌کنیم. همه حالت‌های ممکن را نمایش دهید و احتمال پیشامد A که در آن فقط یک بار پشت بیاید را بیابید.

اما ما در بخون برای شما کلاس نهمی‌ها یک سورپرایز فوق‌العاده داریم. شما می‌توانید تنها در 10 دقیقه و با مطالعه مقاله‌ی تمرینات عربی نهم با جواب، پاسخ تمامی تمرینات عربی نهم را به خوبی یاد بگیرید.

دانش آموزان عزیز این آموزش، کامل ترین آموزش فصل اول ریاضی نهم می باشد که می توانید با آن نمره کامل را کسب کنید و مثال های خوبی را یاد بگیرید. در ضمن برای نمونه سوالات امتحانی هم دیگر نیازی نیست که نگران باشید؛ در بخش نمونه سوال ریاضی نهم برای تمامی فصل ها یک بانک سوال رایگان را برای شما آماده کرده ایم و کافیست از طریق لینک قبلی وارد شوید. منتظر نظرات، سوالات، انتقادات و پیشنهاد شما در این مقاله از طریق بخش نظرات هستیم. همچنین از طریق عناوین زیر می‌توانید به سایر مباحث پایه خود دسترسی داشته باشید:

• نهم
• ریاضی نهم
• آموزش ریاضی نهم

سوالات متداول

• آیا در مقاله آموزش فصل اول ریاضی نهم، مطابق با کتاب های درسی جدید این آموزش آماده شده است؟
  بله! براساس آخرین تغیرات کتاب های درسی آموزش ها تدوین شده اند.
• فصل اول ریاضی نهم شامل کدام مباحث است؟
  مجموعه، اجتماع، اشتراک و تفاصل مجموعه ها، احتمال و نمایش مجموعه ها
• فصل اول ریاضی نهم با کدام یک از فصل ها در سایر پایه ها مرتبط است؟
  با فصل اول ریاضی دهم و فصل هشتم ریاضی هشتم