سلام به همه بخونیهای عزیز و باهوش. امروز در سایت بخون با آموزش فصل چهار ریاضی پنجم همراه شما عزیزان هستیم. ریاضی پایه پنجم از جمله دروسی است که یادگیری آن اهمیت زیادی دارد. اغلب دانشآموزان با مباحث این فصل مشکل دارند و از مطالعه آن فرار میکنند. در ابتدای کار با عنوان مباحث فصل چهار ریاضی پنجم آشنا خواهیم شد و سپس هر مبحث را به طور کامل توضیح خواهیم داد. مباحث فصل چهار کتاب ریاضی پنجم عبارتند از:
- تقارن محوری
- تقارن مرکزی
- زاویه و نیمساز
- چندضلعیها و مجموع زاویههای آنها
شاید با شنیدن اسم این مباحث به شما احساس دلسردی دست پیدا کند و رغبتی برای یادگیری نداشته باشید. اما دوست خوبم ما در سایت بخون میخواهیم تصور شما نسبت به درس ریاضی را تغییر دهیم. ابتدا تک تک مباحث فصل چهار ریاضی پنجم را با زبانی ساده و کامل آموزش میدهیم. سپس با گام به گام فصل چهار ریاضی پنجم تمامی تمرینات کتاب درسی را حل خواهیم کرد. در گام آخر با نمونه سوال فصل چهار ریاضی پنجم شما را به تسلط %100 میرسانیم. پس اصلا نگران نباشید، چون ما در بخون تا شما را به نمره 20 نرسانیم، دست از سرتان برنخواهیم داشت!!! حال کمتر از 10 دقیقه وقت بگذارید و با مطالعه آموزش فصل چهار ریاضی پنجم خود را برای گرفتن نمره 20 درس ریاضی آماده کنید.
تدریس ریاضی مبحث تقارن محوری پایه پنجم دبستان
آموزش فصل چهار ریاضی پنجم را با مبحث تقارن محوری شروع میکنیم. برای شروع آموزش این مبحث ابتدا یک سوال مطرح میکنیم: تقارن محوری به چه معناست؟ جواب این سوال را به این شکل میدهیم: در تقارن محوری قرینه یک نقطه را نسبت به یک خط بدست میآوریم. محور تقارن خطی است که قرینه هر نقطه از شکل را نسبت به آن به خود شکل منطبق میشود. به طور سادهتر میتوان گفت: خطی که شکل را به دو قسمت مساوی تقسیم میکند، محور تقارن است.
حال این سوال مطرح میشود که چگونه برای یک شکل محور تقارن را رسم کنیم؟ قرینه یک نقطه را چگونه نسبت به یک خط بدست بیاوریم؟ برای پاسخ به این سوال باید به نکات بسیار مهمی توجه کنیم. اولین نکته این است که برای رسم محور تقارن باید توجه داشته باشیم که هر دو طرف شکل باید کاملا قرینه باشند. برای بدست آوردن قرینه یک نقطه روشهای مختلفی وجود دارد. با بررسی یک مثال روشهای مختلف بدست آوردن قرینه یک نقطه را بیان میکنیم.
مثال) در هر یک از شکلهای زیر قرینه نقطه «ت» را نسبت به خط تقارن بدست آورید.
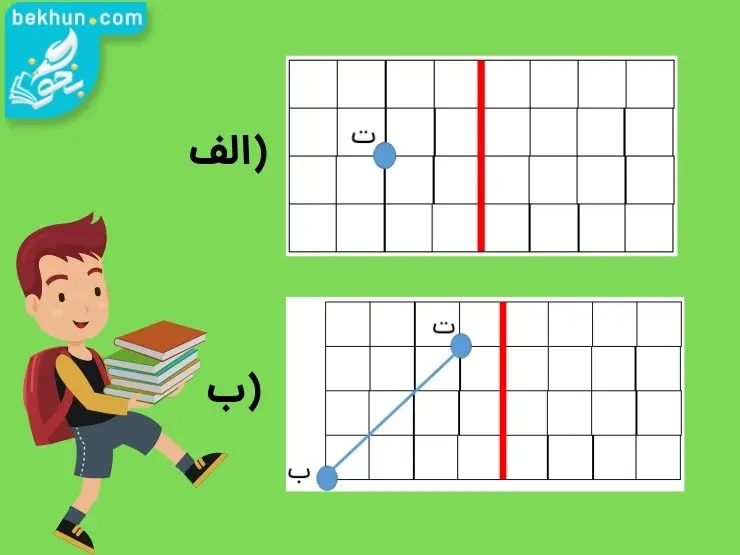
حل: برای پاسخ به این سوال دو راه وجود دارد. راه اول این است که کاغذ شطرنجی را از وسط تا کنیم و به کمک آن مکان نقطه «ت» را در سمت دیگر خط تقارن بیابیم. راه دوم این است که فاصله نقطه «ت» از خط تقارن را اندازه گرفته و مکان این نقطه را در سمت دیگر مشخص کنیم.
الف) در این شکل نقطه «ت» دو خانه با محور تقارن فاصله دارد. پس از مکان این نقطه حرکت کرده و به اندازه دو خانه از سمت راست محور عبور میکنیم. اینجا قرینه نقطه «ت» نسبت به محور تقارن است.
ب) در این شکل یک پارهخط داریم. برای بدست آوردن قرینه این پارهخط کافی است مکان نقاط «ب» و «ت» را بیابیم و با یک خط به هم وصل کنیم. شکل بدست آمده قرینه این پارهخط نسبت به محور تقارن میباشد. پاسخ این سوال را در شکل زیر مشاهده میکنید:
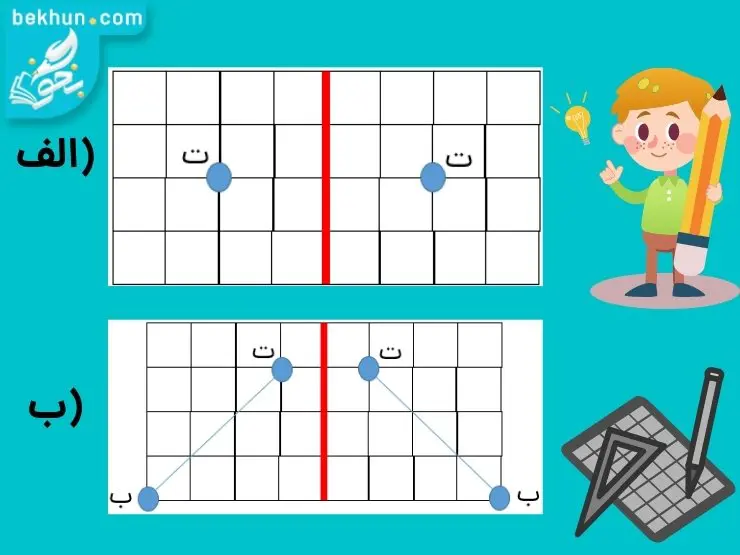
پس با توجه به مثال بالا یاد گرفتیم با نقطهیابی میتوانیم قرینه شکلهای مختلف را بیابیم. اکنون اگر از ما بخواهند خط تقارن یک شکل را رسم کنیم، چگونه باید عمل کنیم؟! خب همانطور که اشاره کردیم خط تقارن یعنی هر دو طرف آن یکسان باشند. با توجه به این نکته خط تقارن چند شکل مختلف را در زیر رسم کردهایم:
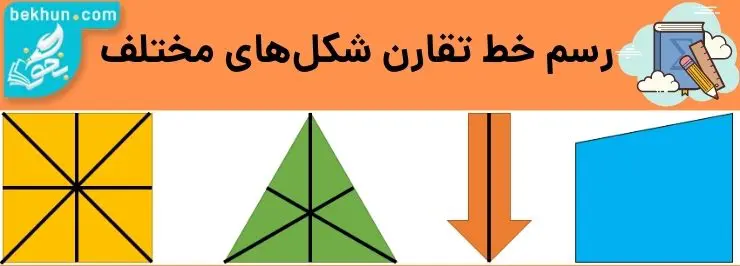
همانگونه که از اشکال بالا مشخص است، یک شکل میتواند چند خط تقارن داشته باشد و یک شکل اصلا خط تقارن ندارد!!! پس همیشه برای هر شکلی خط تقارن نخواهیم داشت.
نکته: دایره بیشمار خط تقارن دارد.
توضیح تقارن مرکزی پایه پنجم
در مبحث قبلی تقارن یک نقطه، پارهخط و شکل را نسبت به یک خط بدست آوردیم. حال در ادامه آموزش فصل چهار ریاضی پنجم به بررسی مبحث تقارن مرکزی خواهیم پرداخت. در اینجا قرینه نقاط، پارهخط و اشکال را حول یک نقطه بدست خواهیم آورد. برای این کار باید شکل مورد نظر را حول نقطه داده شده به اندازه °180 بچرخانیم. برای درک بهتر این موضوع یک مثال برای شما آوردهایم که قرینه هر شکل را نسبت به نقطه «ن» رسم کردهایم:
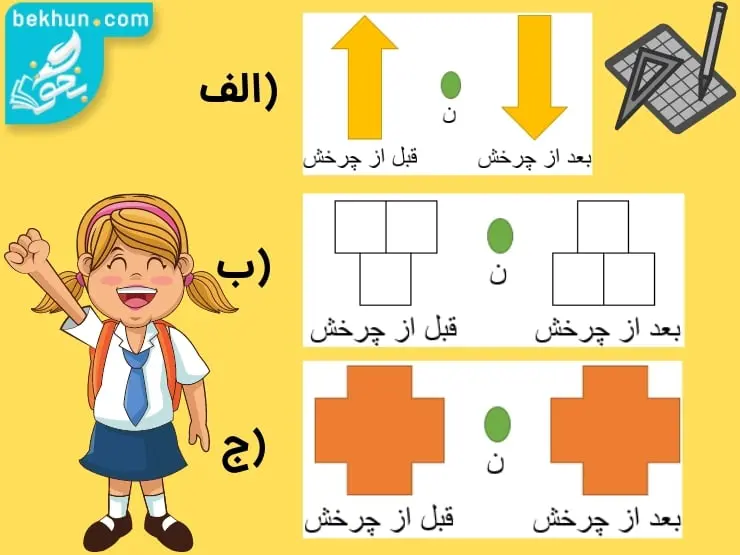
خب همانطور که در شکل مشاهده میکنید، هر یک از اشکال نسبت به نقطه «ن» به اندازه °180 چرخیدهاند. اکنون این سوال برای شما پیش میاید:” چرا شکل قسمت «ج» هیچ تغییری نکرده است؟!!” پاسخ این پرسش یکی از مفاهیم اساسی این فصل را بیان میکند. هرگاه شکلی را نیم دور حول نقطهای بچرخانیم و شکل روی خودش منطبق شود، میگوییم آن شکل تقارن مرکزی دارد. به نقطهای که شکل را حول آن چرخاندیم، مرکز تقارن آن شکل میگویند.
ریاضی پایه پنجم دبستان | آموزش زاویه و نیمساز
یکی از مباحث مهمی که در آموزش فصل چهار ریاضی پنجم به آن میپردازیم، مبحث زاویه و نیمساز است. شما در سالهای قبل با زاویه آشنا شدید و میدانید که هر زاویه از یک راس و دو نیم خط تشکیل میشود. در کتاب ریاضی پنجم شما را با مجموع زوایای داخلی چندضلعی و رسم نیمساز آشنا خواهیم کرد. یادگیری این مباحث بسیار در حل سوالات این فصل به شما کمک میکند. ابتدا از مجموع زوایای یک مثلث شروع خواهیم کرد.
یک مثلث از سه ضلع و سه راس تشکیل شده است. در داخل دفتر خود یک مثلث رسم کنید و سپس با قیچی آن را به سه زاویه جدا از هم تقسیم کنید. اگر این زاویهها را کنار هم بگذارید و روی صفحه دفتر خود قرار دهید، یک زاویه نیم صفحه را مشاهده خواهید کرد. اگر به یاد داشته باشید زاویه نیم صفحه، زاویهای است که از دو زاویه قائمه تشکیل میشود. یعنی زاویه نیم صفحه °180 است. خب از این تعریف به چه نتیجهای خواهید رسید؟!! آفرین درست حدس زدید!!! مجموع زوایای داخلی یک مثلث °180 است.
به کمک همین نتیجه ساده به سوالات زیادی که در مبحث زاویه مطرح میشود، میتوانیم پاسخ دهیم. فقط کافیست که نکته بالا را فراموش نکنید. اکنون میخواهیم به بررسی مثالی بپردازیم تا شما نیز با نحوه حل سوالات زاویه بیشتر آشنا شوید و به تسلط در این مبحث برسید. در هر یک از شکلهای زیر میخواهیم زاویه مجهول سوال را پیدا کنیم:
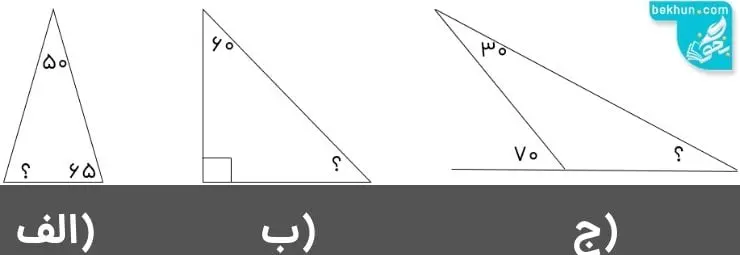
خب دوستان برای حل هر قسمت کافیست دوباره این نکته را یادآوری کنیم: مجموع زوایای داخلی مثلث °180 است.
الف) °65 = 115 – 180 ⇒ °115 = 50 + 65
ب) °30 = 150 – 180 ⇒ °150 = 60 + 90
ج) در مورد این قسمت یک توضیح لازم است. زاویه سمت چپ یک زاویه نیم صفحه است که یک طرف آن 70 درجه است. پس سمت دیگر آن که یکی از زوایای داخلی مثلث است، برابر است با: 110 = 70 – 180. حال با این نکته داریم: °40 = 140 – 180 ⇒ 140 = 30 + 110
اکنون وقت آن است که به سراغ مبحث نیمساز برویم. سادهترین تعریفی که برای نیمساز ارائه میدهیم، به این صورت است: خطی که زاویه را به دو قسمت کاملا مساوی تقسیم میکند و از راس زاویه میگذرد. بیان درستتر این است که نیمساز در واقع نیمخطی است که یک سر آن در راس زاویه قرار دارد و زاویه را به دو قسمت برابر تقسیم میکند.
اکنون با توجه به تعریف نیمساز اندازه هر یک از زاویههای خواسته شده در شکلهای زیر را مشخص کنید.
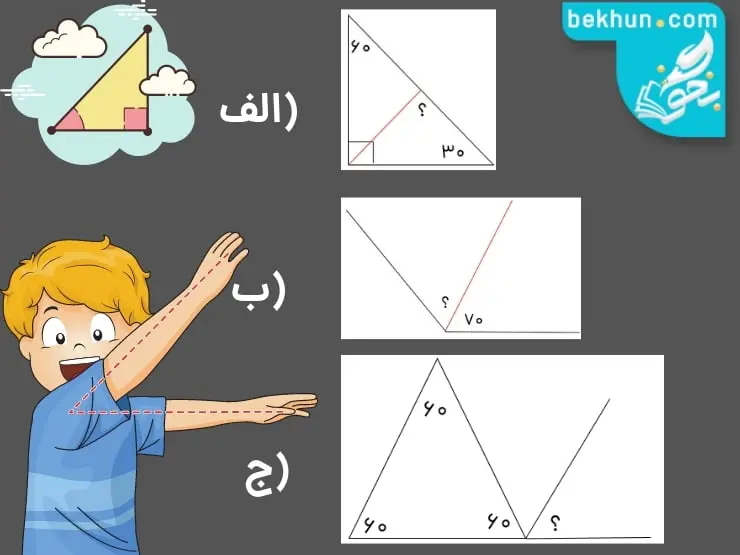
حل: برای حل هر قسمت از دو نکته مربوط به نیمساز و مجموع زوایای داخلی مثلث کمک میگیریم. پس خواهیم داشت:
الف) °105 = 75 – 180 ⇒ 75 = 30 + 45 ⇒ چون نیمساز زاویه قائمه را به دو زاویه 45 درجه تقسیم کرده است.
ب)°70 ⇒ دو طرف نیمساز زاویههای هم اندازه هستند.
ج) °60 = 2 ÷ 120 ⇒ 120 = 60 – 180 ⇒ زاویه نیم صفحه است.
آموزش فصل چهار ریاضی پنجم | چندضلعیها و مجموع زاویههای آنها
آخرین مبحثی که در آموزش فصل چهار ریاضی پنجم بررسی میکنیم، چندضلعیها و مجموع زاویههای آنها میباشد. در مبحث قبلی برای بدست آوردن مجموع زاویههای مثلث یک روش پیشنهاد دادیم. اکنون برای بدست آوردن مجموع زوایای داخلی یک چهار ضلعی نیز از همین روش استفاده میکنیم. اگر زاویههای یک چهار ضلعی را کنار هم قرار دهیم، یک دایره کامل تشکیل میشود. پس مجموع زوایای داخلی هر چهارضلعی °360 است. اکنون میخواهیم برای چهارضلعیها نکات مهمی را به شما آموزش دهیم.
متوازی الاضلاع: 1) در متوازی الاضلاع، ضلعهای رو به رو موازی هستند. 2) ضلعهای رو به رو با هم مساویاند. 3) قطرها یکدیگر را نصف میکنند. 4) متوازی الاضلاع خط تقارن ندارد.
مستطیل: 1)ضلعهای رو به رو موازی هستند. 2) ضلعهای رو به رو با هم مساویاند. 3) قطرها یکدیگر را نصف میکنند. 4) مستطیل دارای 2 خط تقارن است.
مربع: 1) در مربع، ضلعهای رو به رو موازی هستند. 2) ضلعهای رو به رو با هم مساویاند. 3) قطرها یکدیگر را نصف میکنند. 4) قطرها و نیمسازها با هم برابرند. 5) مربع دارای 4 خط تقارن است.
لوزی: 1) در لوزی، ضلعهای رو به رو موازی هستند. 2) ضلعهای رو به رو با هم مساویاند. 3) قطرها یکدیگر را نصف میکنند. 4) قطرها و نیمسازها با هم برابرند. 5) لوزی دارای 2 خط تقارن است.
نکات بیان شده خلاصه بسیار مهمی از مبحث چهارضلعیها در فصل چهار ریاضی پنجم است. با این نکات تمامی سوالات مربوط به این مبحث به آسانی حل خواهد شد. در ادامه با حل یک مثال این مبحث را به طور کامل جمعبندی میکنیم:
مثال) هر یک از موارد مجهول را در هر شکل بیابید.
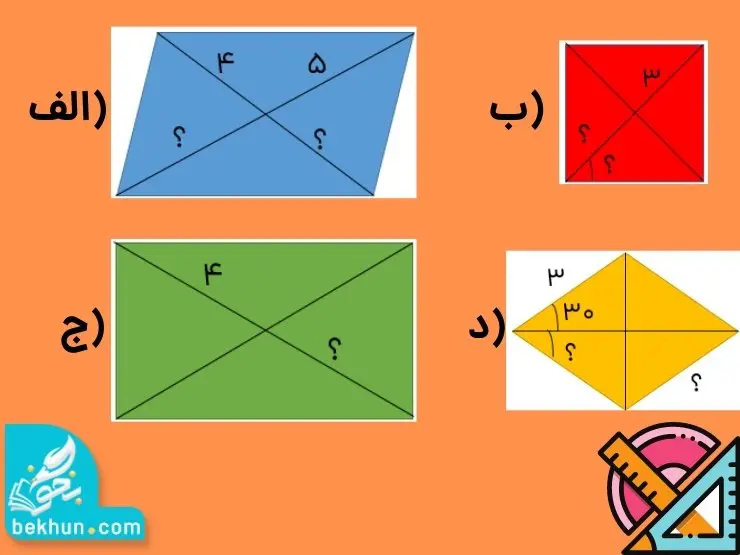
برای حل هر یک از قسمتهای این مثال از نکتههای مربوط به هر شکل استفاده میشود:
الف) همانطور که گفتیم در متوازی الاضلاع، قطرها یکدیگر را نصف میکنند. پس مجهولات سوال به ترتیب 4 و 5 خواهد بود.
ب) در یک مربع، قطرها و نیمسازها با هم برابرند. پس اندازه زاویه مجهول °45 است. همچنین در یک مربع قطرها یکدیگر را نصف میکنند، پس مجهول دیگر سوال برابر با 3 است.
ج) در یک مستطیل قطرها یکدیگر را نصف میکنند، پس مجهول این قسمت برابر با 4 است.
د) در یک لوزی، اضلاع رو به رو مساویاند. پس اندازه ضلع مجهول برابر با 3 است. در لوزی قطرها یکدیگر را نصف میکنند، پس اندازه زاویه مجهول °30 است.
همانطور که از مثال بالا مشخص است، تمامی سوالات این مبحث از فصل چهار ریاضی پنجم به کمک نکاتی که به شما آموزش دادیم، حل میشود.
سخن پایانی
دوستان عزیز به پایان آموزش فصل چهار ریاضی پنجم رسیدیم. امیدواریم که مقاله آموزش فصل چهار ریاضی پنجم مورد توجه شما قرار گرفته باشد. شما عزیزان با عضویت در خبرنامه بخون میتوانید به بهترین مقالات برای تمامی پایههای تحصیلی دسترسی رایگان داشته باشید. همچنین به کمک لینک آموزش ریاضی پنجم ابتدایی تمامی مقالات آموزشی ریاضی پنجم را در اختیار خواهید داشت. در ضمن با کلیک بر روی لینک ریاضی پنجم ابتدایی، به هر آنچه از درس ریاضی پنجم نیاز دارید دسترسی خواهید داشت. دوستان پایه پنجمی برای مشاهده مقالات سایر دروس پایه پنجم، بر روی لینک پنجم ابتدایی کلیک کنید.
در انتها از شما عزیزان میخواهیم که با ثبت انتقادات و پیشنهادات خود در قسمت نظرات، ما را در هرچه بهتر نوشتن مقالات آموزشی یاری کنید. در صورت داشتن رضایت از مقاله آموزش فصل چهار ریاضی پنجم، این مقاله را با دوستان خود به اشتراک بگذارید. همچنین با ثبت ستارههای رنگی آسمان مقاله ما را ستاره باران کنید و باعث انگیزه و دلگرمی ما شوید.
سوالات متداول
- آیا در مقاله آموزش فصل چهار ریاضی پنجم تمامی مباحث را به طور کامل بررسی کردهاید؟
بله، تمامی مطالب فصل چهار ریاضی پنجم را با زبانی ساده بیان کردهایم. - آیا در مقاله آموزش فصل چهار ریاضی پنجم سوالات کتاب درسی نیز حل شده است؟
خیر، برای سوالات کتاب از مقاله گام به گام فصل چهار ریاضی پنجم استفاده کنید. - آیا فایل pdf مقاله آموزش فصل چهار ریاضی پنجم نیز در سایت وجود دارد؟
بله، میتوانید فایل pdf را در انتها همین متن دانلود کنید. - آیا سایر فصلها ریاضی پنجم نیز دارای مقاله آموزشی هستند؟
بله، مقالات آموزش فصل اول ریاضی پنجم، آموزش فصل دوم ریاضی پنجم و آموزش فصل سه ریاضی پنجم نیز در سایت بخون وجود دارد.