سلام به همه دوستان عزیز پایه پنجم. سایت بخون امروز با آموزش فصل سه ریاضی پنجم همراه شما هستیم. همانطور که میدانید در فصل سه ریاضی پنجم با نسبت، تناسب و درصد سر و کار داریم. هر کدام از این مباحث نه تنها در حل سوالات فصل سه بلکه در حل سوالات سایر فصلها نیز به شما کمک خواهند کرد. در واقع مبحث درصد از جمله مباحثی است که تا انتهای دوره تحصیلی برای شما کاربرد دارد. پس یادگیری این مبحث از اهمیت زیادی برخوردار است. در ابتدای کار شما را با مباحث این فصل آشنا خواهیم کرد و سپس هر یک از این مباحث را به طور کامل بررسی خواهیم کرد. فصل سه ریاضی پنجم شامل مباحث زیر است:
- نسبت
- نسبتهای مساوی
- تناسب
- درصد
درس ریاضی یکی از شیرینترین دروسی است که در طول دوره تحصیل با آن رو به رو خواهید شد. داشتن یک آموزش درست و کامل در درس ریاضی باعث میشود که علاقه شما روز به روز به این درس بیشتر شود. شاید اکنون این سوال برای شما پیش بیاید که:“خب آموزش خب از کجا پیدا کنم؟!!” جواب سوال شما نزد ما است، پس لازم نیست که نگران باشید!!! ما در سایت بخون بهترین آموزشهای درس ریاضی را برای شما در نظر گرفتهایم. در ضمن با مقالات گام به گام و نمونه سوال شما را به تسلط کامل در درس ریاضی خواهیم رساند. در بخون تا شما را به نمره 20 نرسانیم، دست از سرتان برنخواهیم داشت!!! امروز میخواهیم با آموزش فصل سه ریاضی پنجم یک هدیه خوب به دانشآموزان پایه پنجم بدهیم. پس کمتر از 10 دقیقه وقت بگذارید و این متن را تا انتها دنبال کنید.
آموزش ریاضی پایه پنجم فصل سوم | نسبت
آموزش فصل سه ریاضی پنجم را از مبحث نسبت شروع خواهیم کرد. شما در طول روز به دفعات فراوان با مبحث نسبت سر و کار دارید. برای مثال هنگام درست کردن شربت یک نسبت مشخص بین مقدار شربت و آب برقرار میکنید. خب اگر این نسبت رعایت نشود، شربت شما یا خیلی شیرین میشود یا خیلی بیمزه!!! واقعیت امر این است که مبحث نسبت بسیار سادهتر از آن است که فکرش را میکنید. با رعایت یک سری قواعد مشخص میتوانید هر نسبتی را به راحتی بدست آورید.
نسبت حاصل یک کسر ساده میباشد. در صورت کسر مقدار جزء خواسته شده را مینویسیم و در مخرج کسر مقدار کل را خواهیم نوشت. برای این که با بدست آوردن نسبت بیشتر آشنا شوید، چند مثال برای شما حل خواهیم کرد. در هر یک از مثالها نسبت مقادیر مختلفی را بدست خواهیم آورد.
مثال1) در یک سالن ورزشی، 10 عدد توپ فوتسال، 5 عدد توپ بسکتبال و 3 عدد توپ والیبال وجود دارد. نسبت هر یک از توپها به کل توپهای ورزشی را بیابید.
حل: در ابتدا تعداد کل توپها را محاسبه میکنیم که برابر است با: 18 = 3 + 5 + 10. در گام بعد نسبت هر یک از توپها را به تعداد کل توپها به آسانی محاسبه خواهیم کرد.
فوتسال: تعداد توپهای فوتسال 10 عدد است و کل توپها 18 عدد است. پس نسبت تعداد توپهای فوتسال به تعداد کل توپها، 10 به 18 است.
بسکتبال: 5 عدد توپ بسکتبال در سالن وجود دارد. تعداد کل توپها نیز 18 عدد است. پس نسبت تعداد توپهای بسکتبال به تعداد کل توپها، 5 به 18 است.
والیبال: 3 عدد توپ والیبال در سالن ورزشی داریم. با توجه به این که تعداد کل توپها 18 است، پس نسبت تعداد توپهای والیبال به تعداد کل توپها، 3 به 18 است.
مثال2) در یک مدرسه از دانشآموزان پایه پنجم امتحان ریاضی گرفته شد. از بین 40 دانشآموزان این مدرسه، 12 نفر نمره بالاتر از 17 کسب کردند. همچنین 18 نفر نمره بین 10 تا 17 کسب کردند و سایر دانشآموزان نمره کمتر از 10 گرفتند. نسبتهای هر یک از بازههای نمره بیان شده را بدست آورید.
حل: در صورت سوال سه بازه برای نمرههای دانشآموزان بیان شده است. از طرفی میدانیم که تعداد کل دانشآموزان 40 نفر است، پس خواهیم داشت:
نمره بالاتر از 17: در این امتحان 12 نفر نمره بالاتر از 17 گرفتند و تعداد کل دانشآموزان 40 نفر است. پس نسبت 12 به 40 برقرار است.
نمره بین 10 تا 17: طبق صورت سوال 18 نفر از دانشآموزان نمره بین 10 تا 17 گرفتند. پس نسبت این تعداد به کل دانشآموزان، 18 به 40 است.
نمره کمتر از 10: تعداد کسانی که نمره کمتر از 10 گرفتند: 10 = (18 + 12) – 40. پس نسبت این تعداد به تعداد کل دانشآموزان، 10 به 40 است.
مثال3) با توجه به شکل زیر، به سوالات پاسخ دهید:
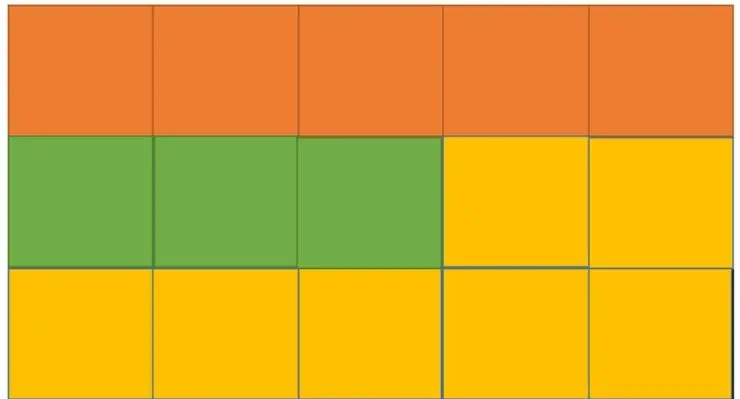
الف) نسبت تعداد مربعهای نارنجی به کل شکل را بدست آورید.
ب) نسبت تعداد مربعهای سبز به کل شکل چقدر است؟
پ) نسبت تعداد مربعهای زرد به کل شکل را بیابید.
حل: در ابتدا تعداد کل مربعهای رنگی را مییابیم که برابر است با: 15 = 7 + 3 + 5. از طرفی از شکل مشخص است که تعداد مربعهای نارنجی 5، تعداد مربعهای سبز 3 و تعداد مربعهای زرد 7 عدد است. اکنون جواب هر یک از سوالات به آسانی بدست میآید:
الف) 5 به 15 ب) 3 به 15 ج) 7 به 15
دوستان عزیز پایه پنجم همانطور که مشاهده کردید هر نسیتی را با دانستن تعداد کل و تعداد جزء به آسانی میتوان بدست آورد. پس در هر سوالی که مطرح شد ابتدا تعداد کل را محاسبه کنید و سپس با توجه به تعداد جزء، نسبت را برقرار کنید.
تدریس نسبتهای مساوی ریاضی پنجم دبستان
در گام اول از آموزش فصل سه ریاضی پنجم با آموزش نسبت و نحوه نوشتن نسبت آشنا شدید. در مرحله بعدی از مقاله آموزش فصل سه ریاضی پنجم به سراغ نسبتهای مساوی خواهیم رفت. حتما به یاد دارید که در مبحث کسر با این سوال رو به رو میشدید:”کسری بنویسید که با کسر زیر برابر باشد؟”. اگر به یاد داشته باشید در ابتدا آموزش فصل سه ریاضی پنجم گفته شد که نسبت یعنی نوشتن یک کسر!!! خب پس همانطور که کسرهای برابر با هم وجود دارد، نسبتهای مساوی نیز نوشته میشود. به کمک این نکته و با ذکر چند مثال مبحث نسبتهای مساوی را مثل آب خوردن یاد میگیرید!!!
مثال1) برای هر یک از کسرهای زیر، چهار کسر مساوی بنویسید.
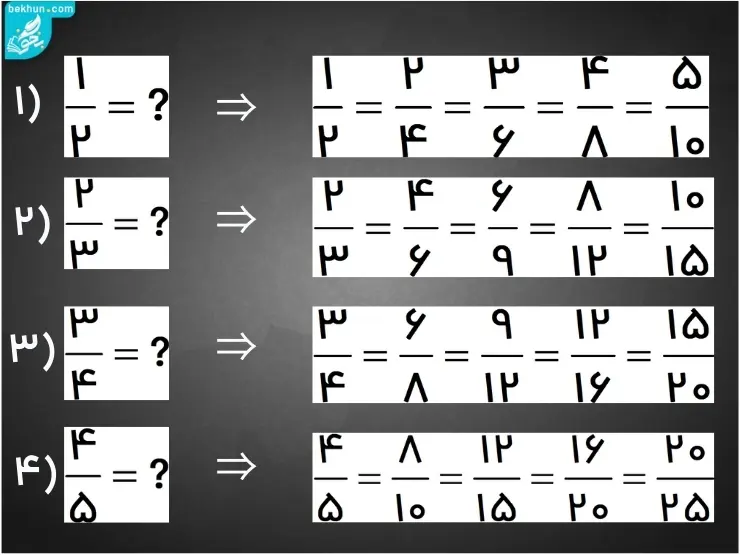
از حل مثال بالا به دو نکته مهم خواهیم رسید:
- اگر صورت و مخرج یک نسبت را در یک عدد ضرب کنیم، نسبتی مساوی با همان نسبت بدست میآید.
- اگر صورت و مخرج یک نسبت را بر یک عدد تقسیم کنیم، نسبتی مساوی با همان نسبت بدست میآید.
مثال2) الف- اگر نسبت دو عدد 2 به 5 باشد و عدد کوچکتر 8 باشد، مجموع این دو عدد چقدر است؟
ب- اگر نسبت دو عدد 4 به 7 باشد و عدد بزرگتر 35 باشد، تفاضل این دو عدد چقدر میشود؟

مثال3) کدام یک از نسبتهای زیر مساویاند؟چرا؟
الف) 16 کامپیوتر برای 40 دانشآموز، 30 کامپیوتر برای 80 دانشآموز ب) 5 راکت تنیس برای 8 نفر، 15 راکت تنیس برای 24 نفر
حل: الف) در جمله اول نسبت 16 به 40 برقرار است و در نسبت دوم نسبت 30 به 80 برقرار است. همانطور که مشخص است مخرج کسر اول یعنی عدد 40 در 2 ضرب شده و مخرج کسر دوم یعنی عدد 80 بدست آمده است. اما صورت کسر اول یعنی عدد 16 با ضرب در عدد 2 برابر 32 میشود، درحالی که صورت کسر دوم عدد 30 میباشد!!! پس این دو نسبت با هم مساوی نیستند.
ب) در جمله اول نسبت 5 به 8 و در جمله دوم نسبت 15 به 24 برقرار است. از ضرب صورت و مخرج کسر اول در عدد 3، صورت و مخرج کسر دوم بدست میآید. پس این دو نسبت با هم مساوی هستند.
همانطور که قول داده بودیم نسبتهای مساوی را به طور کامل بررسی کردیم. رفقای پایه پنجم خسته که نیستید؟!! میخواهیم در ادامه آموزش فصل سه ریاضی پنجم شما را با مباحث جذابی آشنا کنیم.
آموزش فصل سه ریاضی پنجم مبحث تناسب
در مقاله آموزش فصل سه ریاضی پنجم به ایستگاه تناسب میرسیم. شما پیش از با مباحث نسبت و نسبتهای مساوی آشنا شدید. با یادگیری کامل مباحث قبلی مشکلی برای یادگیری مبحث تناسب نخواهید داشت. خب در ابتدای کار ببینیم که اصلا تناسب به چه معناست؟ تعریفی که برای تناسب ارائه میشود، به این صورت است: هر دو نسبت مساوی، یک تناسب را تشکیل میدهند. از این تعریف به این نکته خواهیم رسید که وقتی تناسب برقرار میشود که نسبتهای مساوی داشته باشیم.
در ادامه برای یادگیری بهتر چند مثال را حل خواهیم کرد و به طور کامل توضیح میدهیم. این نکته را هم ذکر کنیم که در درس ریاضی برای آموزش و تفهیم مباحث، بهترین روش حل مثال میباشد.
مثال1) نسبت اندازههای دو زاویه 2 به 7 است. اگر مجموع این دو زاویه 63 درجه باشد، اندازه هر زاویه را بیابید.

در حل این مثال توجه کنید که چون مجموع زاویهها را در صورت سوال داریم، پس نسبتها را جمع میکنبم: 9 = 7 + 2.
مثال2) محیط مستطیلی 180 متر و نسبت طول به عرض آن 6 به 3 است.
الف) اندازه طول و عرض این مستطیل را بیابید.
ب) مساحت این مستطیل را بیابید.
حل: الف) میدانیم محیط یک مستطیل برابر است با: 2 × (طول + عرض). در نتیجه مجموع طول و عرض مستطیل 90 = 2 ÷ 180 میباشد. خب همانطور که در سوال قبل اشاره کردیم، برای مجموع باید نسبتها را نیز جمع کنیم ⇐ 9 = 6 + 3. حال به سادگی با تشکیل یک تناسب، طول و عرض را مییابیم:

ب) مساحت مستطیل برابر است با: مترمربع 1800 = 30 × 60
مثال3) در هر کدام از موارد زیر متناسب بودن مقادیر داده شده را مشخص کنید.
الف) 5 درخت برای 20 دفتر، 10 درخت برای 40 دفتر ب) 20 لیتر بنزین برای 100 کیلومتر، 60 لیتر بنزین برای 270 کیلومتر
حل: الف) در بخش اول نسبت بین درخت و دفتر 5 به 20(به طور سادهتر 1 به 4) است. در بخش دوم تناسب بین درخت و دفتر 10 به 40(همان 1 به 4) است. پس تناسب برقرار است و به ازای هر 1 درخت، 4 دفتر داریم.
ب) نسبت بین لیتر بنزین و مسافت پیموده شده در جمله اول 20 به 100(با ساده کردن کسر 1 به 5) است. در جمله دوم نسبت 60 به 270( 2 به 9) است. در نتیجه واضح است که در این قسمت تناسب برقرار نیست.
آموزش ریاضی پنجم فصل سوم مبحث درصد
ایستگاه پایانی آموزش فصل سه ریاضی پنجم به مبحث درصد اختصاص دارد. هدف از بیان نسبت و تناسب این بود که با کمک این مباحث بتوانیم مبحث درصد را به شما عزیزان آموزش بدهیم. شما در طول روز بارها و بارها کلمه درصد را شنیدهاید. برای مثال معلم میگوید:”10 درصد از کلاس در امتحان ریاضی پایه پنجم نمره 20 گرفتند”. خب این جمله به چه معناست؟آیا یعنی 10 نفر از کلاس در امتحان نمره 20 کسب کردهاند؟ در پایان این مطلب جواب این پرسش را خواهید یافت.
برای تعریف درصد از خود این کلمه کمک میگیریم!!! درصد یعنی حاصلضرب یک نسبت در عدد 100 یا به عبارت دیگر نوشتن یک تناسب با مخرج 100. پس وقتی برای یک نسبت کسری نوشتیم و تناسبی برقرار کردیم، با ضرب کسر حاصل در عدد 100، در واقع درصد آن کمیت را بدست آوردهایم. در زبان ریاضی درصد را با علامت % نشان میدهند. در ادامه همانند سایر مباحث برای مبحث درصد هم تعدادی مثال را بررسی خواهیم کرد تا شما این مبحث را به آسانی یاد بگیرید.
مثال1) یک باشگاه فوتبال 25 بازیکن دارد. 10 نفر از این بازیکنان کمتر از 20 سال سن دارند و 15 نفر آنان بیش از 30 سال سن دارند. مشخص کنید که چه درصدی از بازیکنان این تیم کمتر از 20 سال و چه درصدی بیش از 30 سال سن دارند؟
حل: برای این سوال ابتدا یک کسر مینویسیم که نسبت بین تعداد بازیکنان زیر 20 سال به کل اعضای باشگاه را مشخص کند. سپس یک تناسب بین این کسر و کسری خواهیم نوشت که مخرج آن 100 باشد. با بدست آوردن صورت کسر دوم در واقع درصد بازیکنان زیر 20 سال بدست خواهد آمد. برای درصد بازیکنان بالای 30 زیر سال نیز به همین شکل عمل خواهیم کرد. در شکل زیر پاسخ این سوال را مشاهده میکنید:

مثال2) %60 یک عدد 360 و %25 یک عدد دیگر 20 است. این دو عدد را بیابید.
حل: در این سوال درصد مشخصی از دو عدد را داریم که با تناسب مناسب باید این اعداد را پیدا کنیم. برای یافتن این دو عدد داریم:
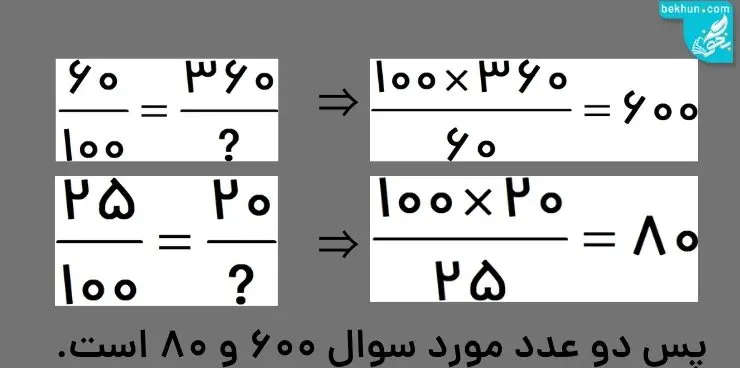
مثال3) %60 دانشجویان یک کلاس 15 نفر است. تعداد کل دانشجویان این کلاس چند نفر است؟ 10 نفر چند درصد از دانشجویان این کلاس است؟
حل: ابتدا با تشکیل یک تناسب مناسب تعداد کل دانشجویان را بدست خواهیم آورد. سپس با یک تناسب دیگر خواهیم فهمید 10 نفر چند درصد از کلاس را تشکیل میدهد:

سخن پایانی
دوستان عزیز پایه پنجم به پایان مقاله آموزش فصل سه ریاضی پنجم رسیدیم. این مقاله اولین گام برای رسیدن به تسلط بر مطالب فصل سه ریاضی پنجم بود. برای تسلط کامل حتما مقالات گام به گام فصل سه ریاضی پنجم و نمونه سوال فصل سه ریاضی پنجم را مطالعه کنید. همچنین برای مطالعه مقالات آموزشی سایر فصلهای ریاضی پنجم کافی است بر روی لینک آموزش ریاضی پنجم ابتدایی کلیک کنید. در ضمن با لینک ریاضی پنجم ابتدایی به تمامی مقالات آموزشی، گام به گام و نمونه سوال ریاضی پنجم دسترسی خواهید داشت. برای اینکه تمامی مقالات پایه پنجم را مشاهده کنید از لینک پنجم ابتدایی استفاده کنید.
شما عزیزان با عضویت در خبرنامه بخون میتوانید به بهترین مقالات آموزشی به طور رایگان دسترسی داشته باشید. دوستان عزیز امیدواریم مقاله آموزش فصل سه ریاضی پنجم مورد توجه شما قرار گرفته باشد و این مقاله را با دوستان خود به اشتراک بگذارید. برای هرچه بهتر شدن مقالات آموزشی انتقادات و پیشنهادات خود را در قسمت نظرات برای ما ارسال کنید. همچنین با دادن ستارههای رنگی به این مقاله باعث دلگرمی و افزایش انگیزه ما شوید.
سوالات متداول
- آیا در مقاله آموزش فصل سه ریاضی پنجم تمامی مطالب را به طور کامل بررسی کردهاید؟
بله، در این مقاله تمامی مباحث فصل سه ریاضی پنجم کامل و دقیق بررسی شده است. - آیا برای سایر فصلها نیز مقاله آموزشی وجود دارد؟
بله، شما میتوانید از مقالات آموزش فصل اول ریاضی پنجم و آموزش فصل دوم ریاضی پنجم نیز استفاده کنید. - فایل pdf مقاله آموزش فصل سه ریاضی پنجم نیز در سایت وجود دارد؟
بله، در پایان همین متن میتوانید فرمت pdf را نیز دانلود کنید.