در فصل اول ریاضی دوازدهم، با ادامه مفاهیم مربوط به تابع در پایههای دهم و یازدهم آشنا خواهیم شد. این فصل هم از حیث بودجهبندی و هم از حیث ارتباط با سایر فصلها از ارزش بالایی برخوردار است. اگر در یادگیری مفاهیم تابع مشکل دارید دیگر نیازی به نگرانی نیست؛ من ناصر گاگمی هستم و امروز در آموزش فصل اول ریاضی دوازدهم تجربی، در خدمت شما هستم و تمامی مطالب را به صورت کامل بررسی و در اختیار شما عزیزان قرار خواهم داد.
شما مفاهیم توابع را در سال دهم و انواع توابع را در سال یازدهم یاد گرفتهاید. در این آموزش فصل اول ریاضی دوازدهم تجربی، نکات تکمیلی را با هم یاد خواهیم گرفت. در آخر این مطلب شما باید به تمامی بحثهای، توابع چند جملهای، صعودی و نزولی بودن توابع، ترکیب توابع و اینکه چگونه وارون توابع را به دست بیاوریم، مسلط باشید. من ناصر گاگمی هستم، سعی میکنم به شما کمک کنم تا در آخر این مقاله به تمامی بحثهای فصل اول ریاضی دوازدهم تسلط داشته باشید. پس تا آخر با ما همراه باشید و استفاده لازم را از این آموزش ببرید. همچنین شما دانشآموزان عزیز میتوانید تستهای فصل اول ریاضی دوازدهم تجربی را در اختیار داشته باشید.
خلاصه آموزش فصل اول ریاضی دوازدهم تجربی
فصل اول ریاضی دوازدهم تابع است، که شامل سه درس زیر میباشد:
- توابع چند جملهای _ توابع صعودی و نزولی
- ترکیب توابع
- تابع وارون
در ادامه با ما همراه باشید تا این سه درس را به خوبی یاد بگیریم.
آموزش توابع چندجملهای ریاضی دوازدهم تجربی
در سالهای قبل با تابعهای ثابت، خطی و درجه دوم آشنا شدهاید. اما در فصل اول ریاضی دوازدهم قرار است با تابع درجه 3 دست و پنجه نرم کنیم و این تابع را هم مثل تابعهای قبلی شکست دهیم. ابتدا یادآوری ای، داشته باشیم بر تابعهای سالهای قبل، سپس با تابع درجه سوم آشنا میشویم.

دوستان عزیز دوازدهمی، پس از اینکه این آموزش را بطور کامل پشت سر گذاشتید،حتما مقالهی گام به گام فصل اول ریاضی دوازدهم | تابع را به خوبی مطالعه کنید، تا هم بخش آموزش و هم بخش سوالات ریاضی دوازدهم فصل اول را به خوبی پشت سر گذاشته باشید.
آموزش تابع درجه 3 ریاضی دوازدهم تجربی
معادله یا تابع درجه سوم، یک چند جملهای است که بیشترین درجه مجهول در آن 3 میباشد. و فرم کلی آن به شکل عکس زیر میباشد. و یکی از حالتهای آن هم در عکس مشاهده میکنید.
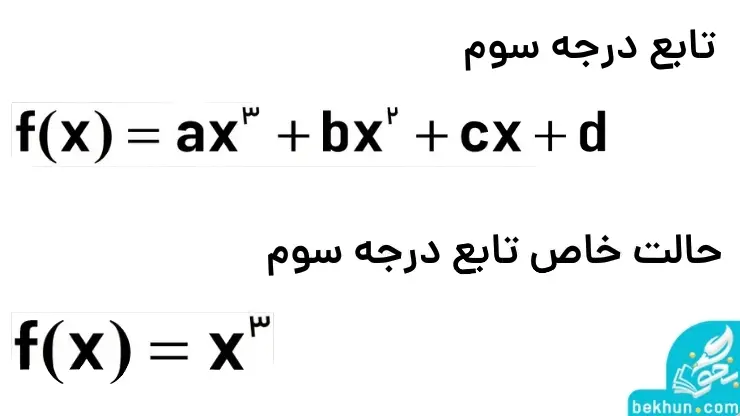
تابع نمونه بالا دارای ویژگیهای زیر میباشد:
- دامنه و برد آن R است.
- نمودار نسبت به مبدا مختصات متقارن است.
- این تابع یک به یک است.
نمودار تابع بالا در شکل زیر نمایش داده شده است.
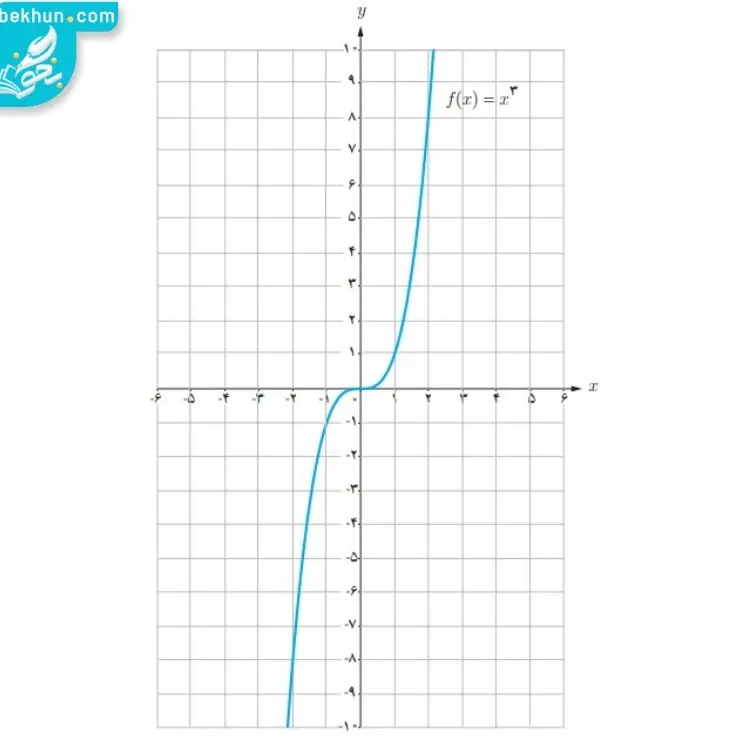
نکات توابع درجه سوم که باید در نظر بگیرید:
- دامنه همه توابع چند جملهای R است. اگر درجه آن فرد باشد برد آن نیز R است.
- به کمک انتقال میتوان توابع درجه سوم را رسم کرد.
- اگر پشت x عدد یا علامت منفی بود ابتدا با x خالی آن را رسم کرده و سپس با جاگذاری علامت و یا عدد آنرا تغییر میدهیم.
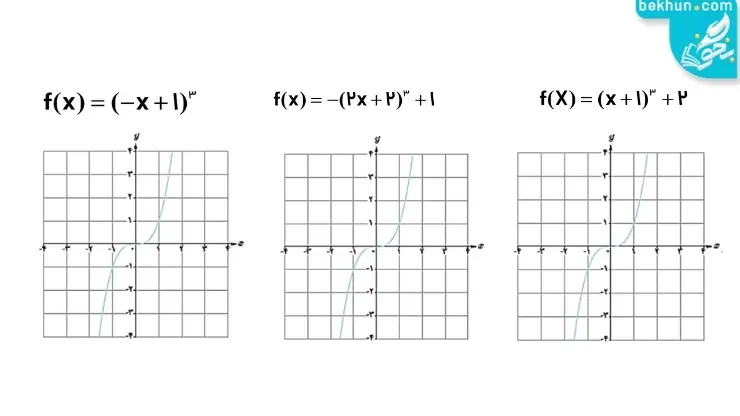
مثال شماره 1: در مثال شماره 1 نمودار چند تابع رسم شده است.
آموزش توابع صعودی و نزولی دوازدهم
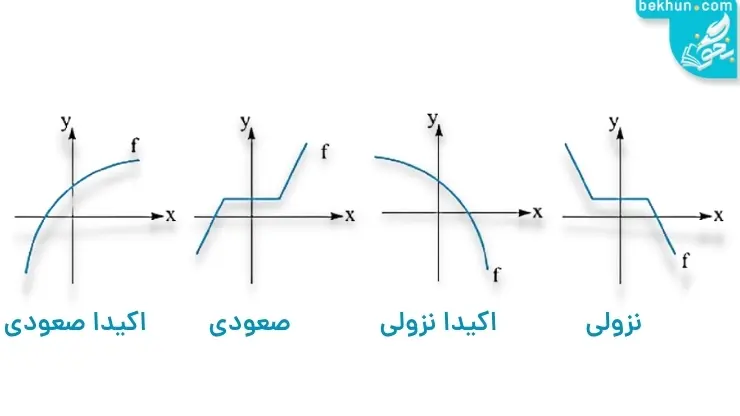
توابع صعودی و نزولی را میتوان به چهار حالت تقسیم کرد. این چهار حالت را میتوان شرایط شما در آزمون آزمایشی که شرکت میکنید مقایسه کرد.
- اکیدا صعودی: شما در هر آزمون آزمایشی که شرکت میکنید، نسبت به آزمون قبلی پیشرفت داشتهاید و آزمون به آزمون تراز شما افزایش پیدا میکند. در این شرایط تراز شما اکیدا صعودی است.
در بازهای که تابع f اکیدا صعودی است، با حرکت روی نمودار از چپ به راست همواره رو به بالا خواهیم رفت، همانند ترازهای شما. - اکیدا نزولی: شما در هر آزمون نسبت به آزمون قبلی پسرفت میکنید ( البته خدای نکرده)، یعنی تراز شما در هر آزمونی که شرکت میکنید پایینتر و پایینتر میآید. در این شرایط تراز شما اکیدا نزولی است.
در بازهای که تابع f اکیدا نزولی است، با حرکت روی نمودار از چپ به راست همواره رو به پایین خواهیم رفت، همانند ترازهای شما. - صعودی: در این شرایط شما در هر آزمون نسبت به آزمون قبلی یا همان تراز را میآورید یا تراز شما بیشتر میشود. یعنی اصلا پسرفت نمیکنید. ( تلاشتان را افزایش دهید که به اکیدا صعودی تبدیل شوید).
در بازهای که تابع f صعودی است، با حرکت روی نمودار از چپ به راست هرگز رو به پایین نخواهیم رفت. - نزولی: شما در هر آزمون که شرکت میکنید اصلا پیشرفت نمیکنید، بلکه فقط پسرفت میکنید و یا همان تراز قبلی را بدست میآورید. ( البته مطئن هستم که این نمیتواند نمودار آزمونهای شما باشد).
در بازهای که تابع f نزولی است، با حرکت روی نمودار از چپ به راست هرگز رو به بالا نخواهیم رفت.
میتوانید از هر یک از تابعهای صعودی و نزولی یک نمونه را در این عکس مشاهده کنید.
دوستان عزیز، اگر در آموزش فصل دوم ریاضی دوازدهم هم مشکل دارید، مقالهی عالی آموزش فصل دو ریاضی دوازدهم | مثلثات را به خوبی مطالعه کنید. تا هم در فصل اول و هم فصل دوم به مهارت کامل دست پیدا کنید.
نکات مربوط به توابع صعودی و نزولی:
- اگر تابعی در کل دامنه خود، اکیدا صعودی و یا اکیدا نزولی باشد، آنگاه آنرا یکنوا میگویند.
- اگر تابع f در کل دامنه خود فقط صعودی و یا نزولی نباشد، به آن غیر یکنوا گفته میشود.
- هر تابع اکیدا صعودی، تابع صعودی هم محسوب میشود.
- هر تابع اکیدا نزولی، تابع نزولی هم محسوب میشود.
- تابعی وجود ندارد که اکیدا صعودی و یا اکیدا نزولی باشد، ولی یک به یک نباشد.
نمونه مثالهای حل شده برای این بخش از سوالهای کتاب است، که میتوانید با مراجعه به مقاله گام به گام فصل اول ریاضی دوازدهم نمونه سوالات حل شده را مشاهده کنید.
آموزش ترکیب توابع ریاضی دوازدهم تجربی
در ریاضی سال یازدهم، با اعمال جبری روی تابع آشنا شدیم، یعنی جمع و تفریق و ضرب و تقسیم توابع، و مطمئن هستم به خوبی آن را فرا گرفتهاید و سراغ این فصل از دوازدهم آمدهاید. امسال با مفهوم ترکیب توابع آشنا خوهیم شد.
اگر f و g دو تابع باشند، ترکیب آنها را با fog یا gof نشان میدهیم. به عبارت ساده یعنی یک تابع را داخل تابع دیگر بریزیم تا ساده شوند. ترکیب تابع را با نماد زیر نشان میدهند و به این معنی است که تابع g را به جای x در f جایگذاری کنیم.

مثال: اگر g={ (1، 2) (3، -1) (2، 0) (-1، 4) (5، -7)} و f={ (0، -1) (5، 2) (3، 5) (-2، 4) }، تابع gof را در صورت امکان بنویسید.
(gof)(0)=g(f(0))=g(-1)=4
(gof)(5)=g(f(5))=g(2)=0
(gof)(3)=g(f(3))=g(5)=-7
(gof)(-2)=g(f(-2))=g(4)=تعریف نشده
gof={ (0، 4) (5، 0) (3، -7) }
ضابطه و دامنه ترکیب توابع ریاضی دوازدهم
برای پیدا کردن fog(x) اول x را داخل تابع درونی g گذاشته سپس، حاصل این جاگذاری را داخل تابع f میگذاریم. اما x باید قابل جاگذاری در g باشد و مقدار تابع قابل جاگذاری در f باشد. بنابراین برای پیدا کردن دامنه تابع مرکب ابتدا دامنه هر یک را پیدا میکنیم، سپس نتیجه هر کدام از قسمتهای تعریف را پیدا کرده و اشتراک میگیریم. یا به زبان ریاضی:
D(fog)={x ∈ Dg | g(x) ∈ Df}
مثال: اگر f(x)=x-2 و g(x)= x2-1، دامنه و ضابطه تابع gof را بدستآورید. ( پاسخ را میتوانید در عکس زیر مشاهده کنید. )
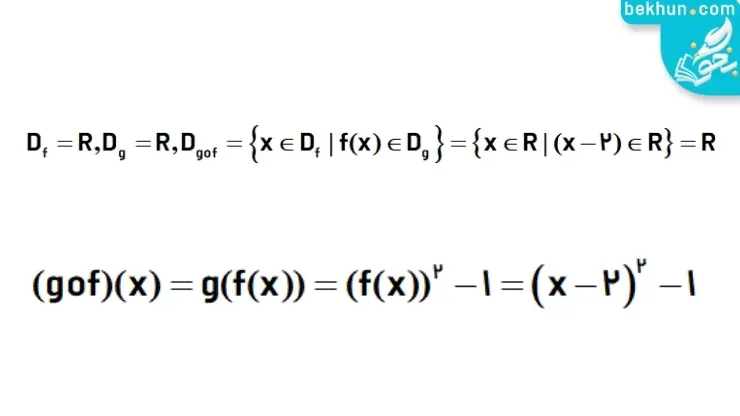
مثال: اگر f(x) و g(x) مطابق تصویر زیر باشند، دامنه و ضابطه fog و gof را محسابه کنید.
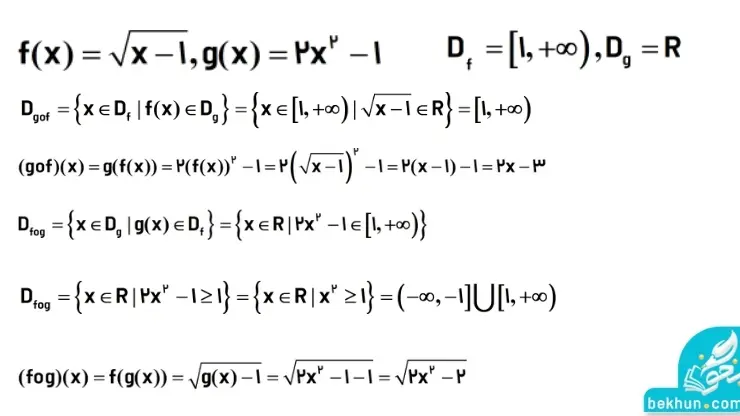
ما برای درس عربی دوازدهم شما دوستان یک مقاله جامع و عالی در نظر گرفتهایم. شما با مطالعه مقالهی معنی درس های عربی دوازدهم، معنی هر 4 درس عربی دوازدهم را بصورت یکجا میتوانید در اختیار داشته باشید.
آموزش معادله با ترکیب توابع در ریاضی دوازدهم تجربی
در این سوالات گاهی پیدا کردن ضابطه ترکیب تابع، سخت است. بنابراین بهتر است از طریق در مرحله زیر سراغ حل اینگونه مسائل برویم:
مرحله اول: معادله fx=a را حل میکنیم.
مرحله دوم: gx را برابر ریشههای بدست آمده از مرحله قبل میگذاریم و جواب را بدست میآوریم.
مثال: اگر f(g(x)) و g(x) مطابق تصویر زیر باشند، آنگاه ضابطه تابع g(x) چقدر است؟
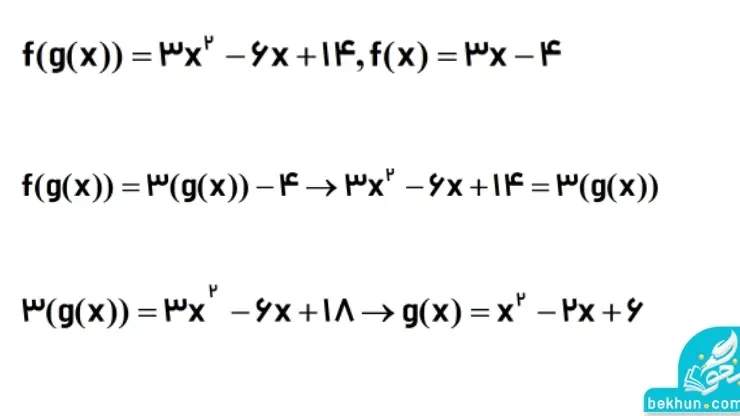
آموزش انتقال توابع در ریاضی دوازدهم تجربی
ما سعی کردیم یک روش ساده را برای آموزش انتقال توابع استفاده کنیم. شما تنها با استفاده از جدول زیر میتوانید همگی سوالات مربوط به این بخش را به آسانی حل کنید.
| مختصات | تقدیر | تاثیر | تغییر |
| (x-a,y) | انتقال قرینه علامت a در محور x | محور x | fx→f(x+a) |
| (x/k,y) | انبساط یاانقباض به اندازه 1/k در محور x | محور x | fx→fkx |
| (-x,y) | قرینه نسبت به محور y | محور x نسبت به y | fx→f(-x) |
| (x,y+1) | انتقال هم علامت a در محور y | محور y | fx→f(x)+a |
| (x,ky) | انبساط یا انقاض به اندازه k در محور x | محور y | fx→kf(x) |
| (x,-y) | قرینه نسبت به محور x | محور y نسبت به x | fx→-f(x) |
| (|x,|y) | قسمت زیر محور y قرینه شود به بالا | محور y | |fx→|fx |
آموزش فصل اول ریاضی دوازدهم تجربی | وارونپذیری و تابع وارون
اگر در تابعی مثل fx مولفههای هر زوج مرتب مانند A(a، b) را با هم عوض کنیم، یعنی به حالت A، (b، a) تابع دیگری ساخته میشود که به آن تابع وارون میگویند و آن را با fx-1 نشان میدهند. بنابراین در fx و fx-1 که آنها را وارون هم مینامیم، جای برد و دامنه با همدیگر عوض خواهد شد.
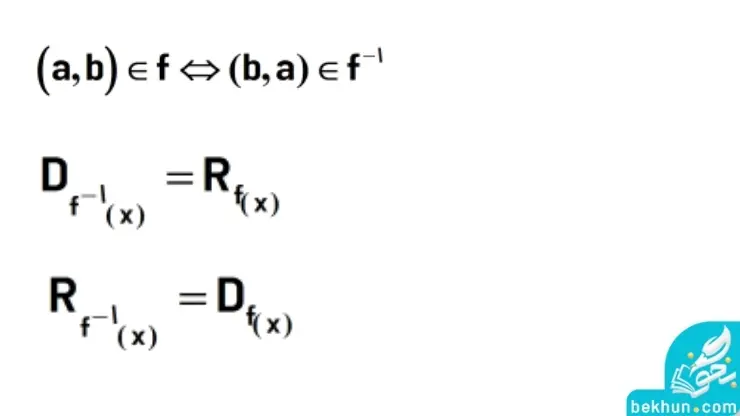
وارونپذیری یک تابع
تابع وارونپذیر یا قابل معکوس شدن است که، فقط یک به یک باشد یعنی برای هر x فقط یک y وجود داشته باشد. پس تابعی که یکنوا است، یک به یک نیز میباشد پس وارونپذیر است.
نکته: هرجا در تستی گفته شد، تابع اکیدا یکنوا بدانید که هم یک به یک است هم وارونپذیر.
مثال: ضابطه تابع زیر را بدستآورید و دامنه و برد بدستآورید.
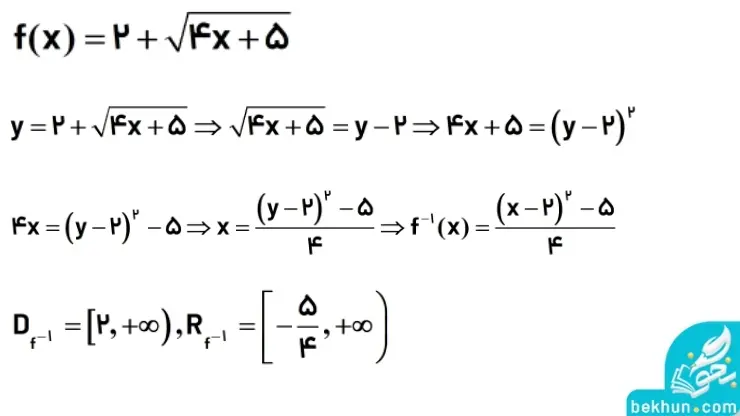
نمودار تابع وارون
نقطه A(a، b) روی تابع f(x) قرار دارد و اگر تابع را وارون کنیم، نقطه A، (b، a) روی تابع f-1(x) قرار میگیرد. میدانیم نقاط A وA، نسبت به نیمساز ناحیه اول و سوم y=x قرینه میباشند. نمودار تابع معکوس f-1(x) قرینه نمودار تابع یک به یک f(x) نسبت به نیمساز ناحیه اول و دوم است، یا به عنوانی دیگر برای رسم تابع f-1(x) آن را نسبت به خط y=x قرینه میکنیم.
در توابع صعودی برای پیدا کردن محلهای برخورد یا تلاقی دو تابع f(x) و f-1(x) که بر روی خط y=x میباشند. کافیست یکی از آنها را y=x تلاقی بدهیم یعنی بنویسیم: f(x)=x و f-1(x)=x. در توابع نزولی ممکن است این نقاط روی این خط قرار نداشته باشند.
دوستان خوبم اگر پس از به پایان رساندن این مقاله، به حل نمونه سوالات بیشتری نیاز داشتید، حتما مقالهی نمونه سوالات فصل اول ریاضی دوازدهم را مطالعه کنید.
مثال: دامنه و برد تابع f و f-1 را بدستآورید و نمودار آن را رسم کنید، همچنین ضابطه f-1 را نیز بدست آوردید.
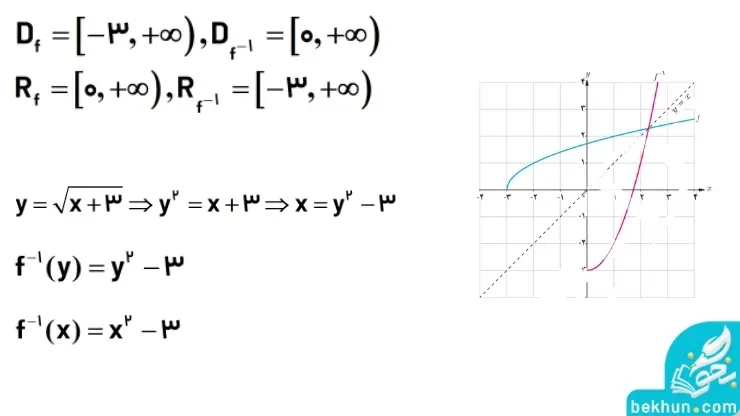
یافتن ضابطه تابع وارون
برای یافتن ضابطه یک تابع یک به یک به ترتیب زیر عمل میکنیم:
- مرحله اول: برد تابع را مییابیم.
- مرحله دوم: جای حروف انگلیسی x و y را عوض میکنیم.
- مرحله سوم: با جابجا کردن حروف و اعداد در دو طرف مساوی، y را در سمت چپ به تنهایی قرار میدهیم.
- مرحله چهارم: به جای y نماد f-1(x) را قرار میدهیم سپس برد تابع f(x) را به عنوان دامنه تابع معکوس در مقابل آن قرار میدهیم.
اما این دو نکته را هم به یاد داشته باشید:
- حتما دامنه تابع معکوس را جلوی ضابطه آن بنویسید.
- وارون تابع خطی با معادله y=ax+b به کمک برعکس کردن اعمال ریاضی به سرعت بدست میآید.
مثال: ضابطه تابع وارون، f(x) و g(x) را بدستآورید، سپس دامنه و برد هر تابع و وارون آن را پیدا کنید.

این آموزش هم به پایان رسید، سعی کریدم مفهوم این فصل را به سادگی به شما یاد بدهیم. امیدوارم مثل تابع اکیدا صعودی در درس ریاضی خود پیشرفت داشته باشید. همچنین از طریق عناوین زیر میتوانید به سایر مباحث پایه خود دسترسی داشته باشید:
سوالات متداول
- آیا در مقاله آموزش فصل اول ریاضی دوازدهم، مطابق با کتابهای درسی جدید این آموزش آماده شده است؟
بله! براساس آخرین تغیرات کتابهای درسی آموزشها تدوین شدهاند. - فصل اول ریاضی دوازدهم شامل کدام مباحث است؟
توابع چندجملهای، توابع صعوی و نزولی، ترکیب توابع و تابع وارون - فصل اول ریاضی دوازدهم با کدام یک از فصلها در سایر پایهها مرتبط است؟
با با فصل دوم ریاضی یازدهم و فصل پنجم ریاضی هشتم - آیا آموزش سایر درسهای سال دوازدهم نیز در سایت قرار دارند؟
بله، نه تنها آموزش دروس دوازدهم بلکه آموزش تمامی دروس همه پایهها در سایت بخون بطور کامل قرار داده شدهاند.