آموزش فصل دو ریاضی دوازدهم | مثلثات

سلام همراهان همیشگی سایت بخون، من ناصر گاگمی این بار با مبحث آموزش فصل دو ریاضی دوازدهم همراه شما عزیزان هستم، امیدوارم که با بی نهایت انرژی تا انتها این بحث با من همراه باشید. شما در سال‌های دهم و یازدهم با دایره مثلثاتی و محور سینوس‌ها و کسینوس‌ها آشنا شده‌اید، حالا در فصل دوم ریاضی دوازدهم با عنوان مثلثات با مطالب جدیدی چون تناوب و تانژانت و معادلات مثلثاتی آشنا خواهیم شد. اصلا نگران نباشید، اگر در یادگیری مفاهیم مثلثات مشکل دارید دیگر نیازی به نگرانی نیست، تا انتهای مقاله با من همراه باشید تا به خوبی برای امتحان آماده شوید. همچنین به شما پیشنهاد می‌کنم آموزش فصل یک ریاضی دوازدهم را نیز مطالعه کنید، که در بخش آموزش ریاضی دوازدهم قرار دارد.

آموزش درس تناوب و تانژانت ریاضی دوازدهم

مطابق شکلی که در زیر به نمایش درآمده است، نمودار تابع های sinx و cosx در فاصله‌هایی ( بازه‌هایی) به اندازه ∏2 تکرار شده است. یعنی فقط اگر یک قسمت از این نمودار را با اندازه ∏2 داشته باشیم، می‌توانیم با کنار هم قرار دادن این قسمت تمامی نمودار را بسازیم.

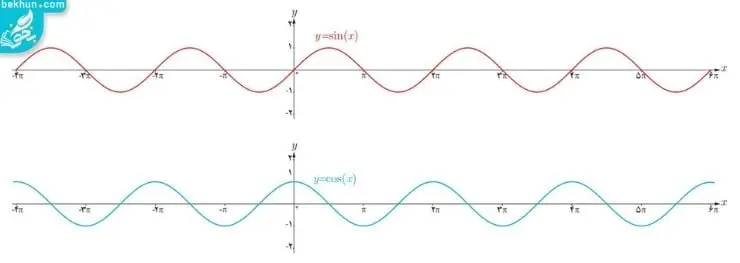
دوره تناوب توابع مثلثاتی ریاضی دوازدهم

تعریف: تابع f را متناوب می‌گوییم، هرگاه یک عدد حقیقی مثبت مانند T موجود باشد بطوری که برای هر x∈D_{f داشته باشیم: f(x±T)=f(x)
کوچکترین عدد مثبت T با این خاصیت را دوره تناوب f گویند.}

کلاس دوازدهمی‌های عزیز به شما پیشنهاد می‌کنم که حتما بعد از به پایان رساندن این مقاله، گام به گام فصل دو ریاضی دوازدهم | مثلثات را نیز به خوبی مطالعه کنید. تا پاسخ تمامی سوالات داخل کتاب این فصل را نیز یاد بگیرید.

محاسبه دوره تناوب توابع مثلثاتی ریاضی دوازدهم تجربی

در کل دوره تناوب در ضابطه توابع مثلثاتی تنها به ضریب x کمان نسبت مثلثاتی ( یعنی تمام آن چیزی که داخل پرانتز قرار دارد ) بستگی دارد و از طریق روابط زیر بدست خواهد آمد. اعدادی که باعث تغییر برد تابع شود هیچ تاثیری بر روی دوره تناوب تابع ندارند. فقط و فقط تنهای عددی که می‌تواند باعث انبساط یا انقباض دوره تناوب شود (a) است.

ماکزیمم و مینیمم تابع‌های سینوسی و کسینوسی ریاضی 3

یافتن ماکزیمم و مینیمم توابع سینوس و کسینوس بسیار ساده است.اگر دامنه این توابع دارای یک دوره تناوب کامل و یا بیشتر از آن باشد آنگاه از دو قاعده زیر پیروی خواهد کرد:

• max= |a|+c
• min= -|a|+c

اگر برای فصل دوم ریاضی هفتم نیاز به حل کردن نمونه سوالات بیشتری دارید، پس مقاله‌ی نمونه سوال فصل دو ریاضی دوازدهم | مثلثات را هم به خوبی این مقاله مطالعه کنید.

مثال: دوره تناوب و مقادیر ماکزیمم و مینیمم توابع زیر را پیدا کنید.

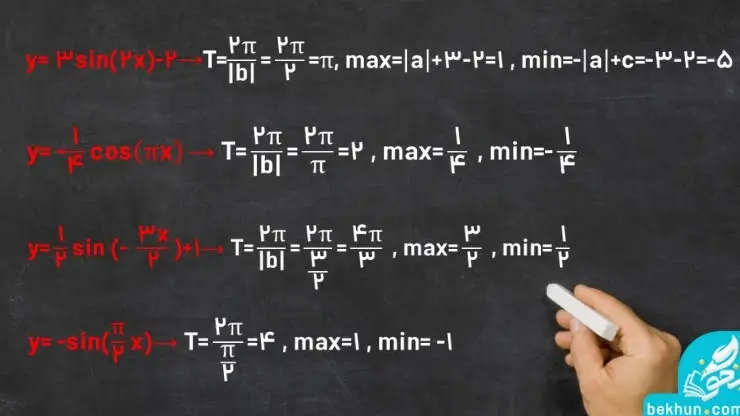
روش محاسبه تابع‌های سینوسی و کسینوسی ریاضی دوازدهم

برای محاسبه و پیدا کردن تابع هایی به شکل y=a sinx(bx)+c یا y=a cosx(bx)+c باید 4 مورد زیر را به خوبی رعایت کرد:

• می‌دانیم دوره تناوب تابع از ضابطه T=2π/|b| بدست می‌آید، که می‌توان از آن b را استخراج کرد.
  در توابع کسینوسی مثبت یا منفی بدست آمدن b اصلا مهم نیست چون کسینوس cos(-x)= cosx منفی خور است.
  در توابع سینوسی مثبت یا منفی بودن b باعث خواهد شد که شکل عادی باشد یا نسبت به محور x قرینه باشد زیرا: sin(-x)= -sinx
• از قبل می‌دانیم که مینیمم و ماکزیمم توابع سینوسی و کسینوسی از دو رابطه max= |a|+c و min= -|a|+c بدست می‌آید.
• در تابع y= a cos(bx)+c اگر a<0 باشد آنگاه، شروع تابع قرینه تابع y= cosx خواهد بود.
• در تابع y= a sin(bx)+c اگر a<0 باشد آنگاه، شروع تابع قرینه تابع y= sinx خواهد بود.

مثال: لطفا مثال صفحه 35 کتاب ریاضی خود را به خوبی مطالعه کنید.

تانژانت (شیب)

در سال‌های قبل با سینوس و کسینوس و نمودار آنها روی دایره مثلثاتی آشنا شده بودیم، اما حالا نوبت به تانژانت میرسد که به بررسی آن بپردازیم.

تابع تانژانت روی دایره مثلثاتی خطی موازی سینوس است که از انتهای سینوس شروع می‌شود. برای پیدا کردن تانژانت هر زاویه‌ای ضلع آنرا امتداد می‌دهیم تا محور تانژانت را قطع کند. سپس فاصله آن از مبدا تابع تانژانت یعنی A را بدست می‌آوریم که در قسمت بالایی دایره مثلثاتی مثبت و در قسمت پایینی منفی است.

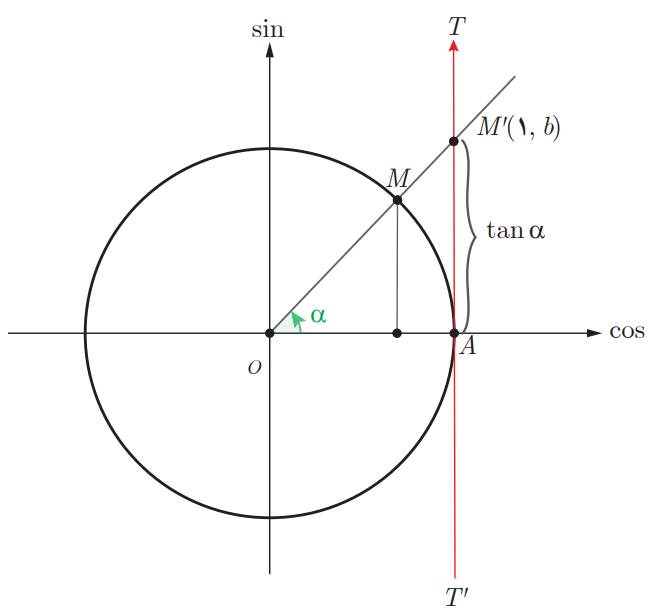
اگر زمان کافی برای پیدا کردن پاسخ سوالات نمونه بیاورید هویت دوازدهم خود ندارید. پس مقاله‌ی جواب نمونه بیاوریدهای هویت اجتماعی دوازدهم را به خوبی مطالعه کنید.

نمودار تابع تانژانت

نکته: برد تانژانت شامل اعداد حقیقی می‌باشد.

نکته: این تابع یعنی تابع تانژانت محور xها را در نقاطی به طول kπ قطع می‌کند.

نکته: در حالت کلی همیشه |tanx|>|sinx| چون در دایره مثلثاتی اندازه پاره خط tanx از پاره خط sinx بیشتر است.

بنابراین تابع f(x)= tanx در کل یک تابع غیریکنوا است، ولی در بازه‌هایی که در آن نقاط تعیف نشده تانژانت که در بالا گفته شد وجود نداشته باشد، اکیدا صعودی است. یعنی در هر یک از 4 ربع دایره مثلثاتی، تانژانت اکیدا صعودی است.

مثال: برای حل مثال از این بخش صفحه 39 از کتاب درسی خود را به خوبی مطالعه کنید.

معادلات مثلثاتی | حل معادلات مثلثاتی

هدف از حل معادلات مثلثاتی پیدا کردن تمام زوایایی است که جاگذاری آنها در معادله پاسخ درست خواهد داد. برای حل معادلات مثلاتی از 3 روش استفاده می‌شود، که در ادامه به بررسی هر کدام از این روش ها می‌پردازیم.

حالت اول حل معادله مثلثاتی | sinx=a

در این حالت معادله وقتی جواب دارد که a بین دو عدد 1 و -1 قرار داشته باشد، یعنی خارج ار محدوده مقدار سینوس معادله هیچ جوابی ندارد. در اینصورت زاویه‌‌ای که سینوس آن a خواهد شد را به جای a در معادله قرار می‌دهیم، و از رابطه زیر جواب کلی معادله را بدست می‌آوریم. ( در فرمول زیر به جای k هر عدد صحیح دلخواه میتوان گذاشت تا جواب جزئی پیدا شود. ).

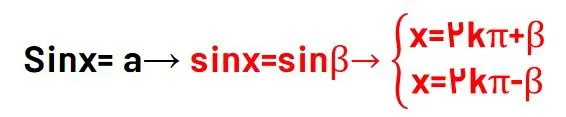
نکته مهم: معادلات خاص سینوس به شکل زیر می‌باشند.

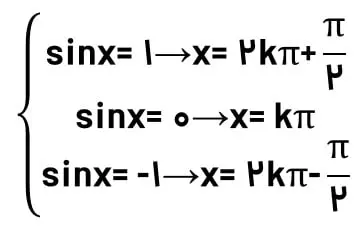
نکته: میدانیم sin(-x)= -sinx، پس اگر عدد منفی بود، علامت منفی مستقیما وارد پرانتز سینوس می‌شود.

یکی از بهترین مقالات جامع بخون برای پایه دوازدهم، جواب تمرینات عربی دوازدهم می‌باشد. شما در این مقاله می‌توانید پاسخ تمامی تمرینات عربی دهم را در چند دقیقه یاد بگیرید.

مثال: معادلات مثلثاتی زیر را حل کنید.

حالت دوم حل معادله مثلثاتی | cosx=a

در این نوع هم مانند حالت اول معادله هنگامی جواب دارد که a در بین 1 و -1 قرار داشته باشد، یعنی خارج از محدوه کسینوس ها، معادله هیچ جوابی ندارد. در این صورت زاویه‌ای که کسینوس آن a می‌شود را در جای a قرار داده و از رابطه زیر جواب کلی معادله را خواهیم نوشت. ( در فرمول زیر به جای k هر عدد صحیح دلخواه میتوان گذاشت تا جواب جزئی پیدا شود. )

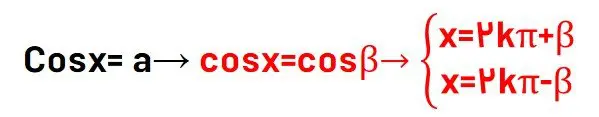
نکته: معادلات خاص کسینوس به شکل زیر می‌باشند.

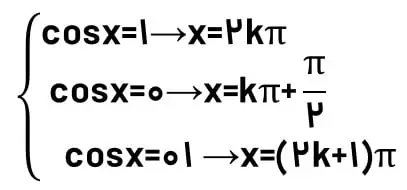
نکته: می‌دانیم cos(x)=cos(Π-x)-، پس اگر عدد منفی بود علامت منفی غیر مستقیم و با محافظت Π وارد پرانتز کمان کسینوس می‌شود.

نکته: در حل معادلات مثلثاتی اگر به جایی رسیدیم که یک طرف سینوس و طرف دیگر کسینوس بود، می‌توانیم به کمک زوایای متمم و با محافظت Π/2 دو طرف را به یک نسبت تبدیل می‌کنیم.

مثال: معادلات مثلثاتی زیر را حل کنید.

دانشآموزان عزیز رشته تجربی پایه دوازدهم، برای درک عمیق‌تر و بهتر از فصل اول زیست دوازدهم، حتما مقاله‌ی آموزش فصل اول زیست دوازدهم | مولکول‌های اطلاعاتی را به خوبی مطالعه کنید.

حالت سوم حل معادله مثلثاتی | tanx=a

این معادله به ازای هر عدد حقیقی a جواب دارد. در اینصورت زاویه‌ای که تانژانت آن a می‌شود را در جای a قرار داده و از رابطه زیر جواب کلی معادله را خواهیم نوشت. ( در فرمول زیر به جای k هر عدد صحیح دلخواه میتوان گذاشت تا جواب جزئی پیدا شود. )

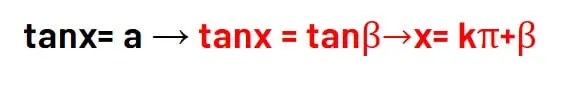
نکته: می‌دانیم tan(-x)= -tanx، پس اگر عدد منفی بود، مشابه سینوس، علامت منفی مستقیما وارد پرانتز کمان تانژانت می‌شود.

نسبت‌های مثلثاتی زوایای دو برابر

باید بدانیم و از یاد نبریم که sin(2α)≠2sin، بنابراین باید روابط زیر را برای 2α نوشت:

مثال: نسبت های مثلثاتی زاویه 22/5 را بدست آورید.

کلام آخر

دوستان عزیز،این مقاله کامل ترین آموزش فصل دو ریاضی دوازدهم تجربی می‌باشد که می توانید با آن نمره کامل را کسب کنید و مثال های خوبی را یاد بگیرید. در ضمن برای نمونه سوالات امتحانی هم دیگر نیازی نیست که نگران باشید؛ در بخش نمونه سوال ریاضی دوازدهم برای تمامی فصل ها یک بانک سوال رایگان را برای شما آماده کرده ایم و کافیست از طریق لینک قبلی وارد شوید. منتظر نظرات، سوالات، انتقادات و پیشنهاد شما در این مقاله از طریق بخش نظرات هستیم. از طریق عناوین زیر هم می‌توانید به کل مطالب مربوط به هردسته به صورت کاملا رایگان دسترسی داشته باشید:

• گام به گام ریاضی دوازدهم
• ریاضی دوازدهم
• دوازدهم

سوالات متداول

• آیا در مقاله آموزش فصل دو ریاضی دوازدهم، مطابق با کتاب های درسی جدید این آموزش آماده شده است؟
  بله! براساس آخرین تغیرات کتاب های درسی آموزش ها تدوین شده اند.
• فصل دو ریاضی دوازدهم شامل کدام مباحث است؟
  تناوب و تانژانت، معادلات مثلثاتی
• فصل دو ریاضی دوازدهم با کدام یک از فصل ها در سایر پایه ها مرتبط است؟
  فصل چهارم ریاضی یازدهم و فصل دوم ریاضی دهم