سلام به همه دوستان عزیز پایه دهم. امروز در سایت بخون میخواهیم با آموزش فصل دو ریاضی دهم غوغا به پا کنیم. همانطور که میدانید، فصل دو ریاضی دهم مربوط به مبحث مثلثات است. این فصل از کتاب ریاضی دهم شامل سه درس میباشد که در این مقاله به طور کامل و با زبانی ساده آنها را بررسی خواهیم کرد. در ابتدا با عنوان مباحث فصل دو آشنا شویم و سپس هر یک را به صورت دقیق بررسی کنیم. مباحث این فصل عبارتند از:

به خوبی به خاطر دارم که در زمان تحصیل خود من نیز برخی از دوستانم با شنیدن کلمه مثلثات، یک غول سرسخت و بزرگ برایشان تداعی میشد. اما خب واقعیت این است که با داشتن یک منبع درست برای یادگیری و حل تمرین، مبحث مثلثات یکی از شیرینترین مباحث درس ریاضی میشود. حال از خود میپرسید: “خب من منبع خوب که کامل و روان توضیح داده باشه رو از کجا پیدا کنم؟!” اصلا لازم نیست نگران نباشید و ترس به دل خود راه ندهید!!! در سایت بخون به صورت قدم به قدم بر مباحث درس ریاضی مسلط خواهید شد. من میلاد خالدیان امروز بهترین آموزش فصل دو ریاضی دهم را برای شما دانشآموزان عزیز تهیه کردهام. به شما قول میدهم که با مطالعه این مقاله دیگر از شنیدن نام مثلثات نخواهید ترسید. پس کمتر از 15 دقیقه وقت بگذارید و مباحث فصل دو ریاضی دهم را مثل آب خوردن سر بکشید!!!
درضمن اگر در بازه زمانی نزدیک به امتحانات پایان ترم خود هستید و به دنبال نمونه سوال جهت آمادگی امتحانات هستید توصیه میکنم از نمونه سوالات نوبت دوم ریاضی دهم با جواب استفاده کنید که یک بانک سوالات امتحانی فوقالعاده بهصورت کاملا رایگان برای شما آماده شده است و به شدت میتواند مفید باشد.
تدریس فصل دوم ریاضی دهم تجربی نسبتهای مثلثاتی
اولین مبحثی که در آموزش فصل دو ریاضی دهم بررسی خواهیم کرد، مبحث نسبتهای مثلثاتی است. مثلثات شاخه گستردهای از علم ریاضی است که به بررسی روابط بین زاویهها اضلاع یک مثلث میپردازد. مبحث مثلثات در علوم دیگری همچون فیزیک، نقشهبرداری و نجوم نیز کاربرد دارد. به کمک مثلثات میتوانیم فاصلهها را به صورت غیرمستقیم اندازه بگیریم.
خب قبل از ورود به مبحث نسبتهای مثلثاتی به یادآوری مبحث تشابه بین دو مثلث خواهیم پرداخت. همانطور که در سالهای قبل آموختید هرگاه در دو مثلث زوایای نظیر برابر و نسبت اضلاع متناظر نیز برابر هم باشند، این دو مثلث متشابه خواهند بود. در نتیجه اگر دو مثلث متشابه باشند، نسبت اضلاع متناظر آنها برابر و زوایای نظیر نیز برابر خواهند بود. با توجه به شکل این مطلب را به صورت ریاضی نیز خواهیم نوشت.

در هندسه ثابت میشود: هرگاه دو زاویه از مثلثی، با دو زاویه از مثلث دیگر برابر باشند، آن دو مثلث، متشابهاند.
نکته بسیار مهم: هرگاه در دو مثلث قائمالزاویه یک زاویه از مثلث ABC با یک زاویه از مثلث DEF برابر باشد، نسبت اضلاع متناظر این مثلث با هم برابر است.
نسبتهای مثلثاتی
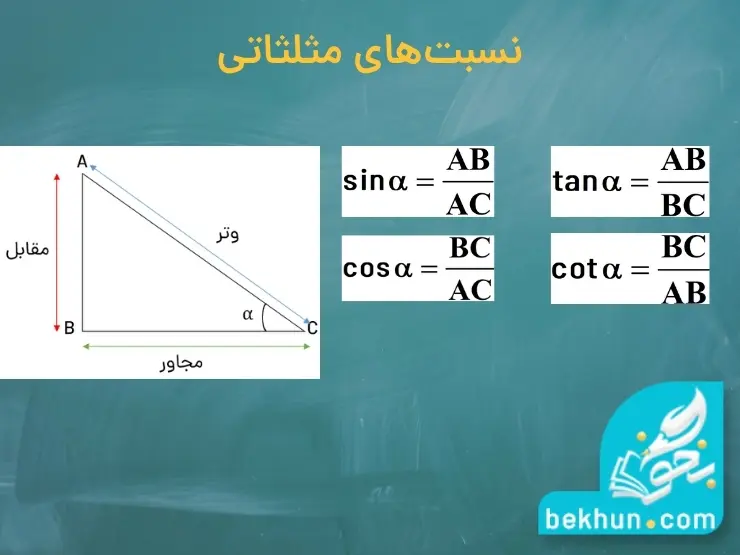
حال وقت آن رسیده که با نسبتهای مثلثاتی sin , cos , tan , cot آشنا شویم. هر یک از این نسبتها را به صورت تصویری و با مثالهای محتلف توضیح خواهیم داد. کاربرد هر یک از این نستهای مثلثاتی را نیز بیان میکنیم. مبحث نسبتهای مثلثاتی یکی از جذابترین مباحث درس ریاضی است که با هم به سراغ یادگیری آن میرویم. ابتدا برای هر یک از نسبتهای مثلثاتی تعریفی ارائه خواهیم کرد و سپس از روی شکل هر یک را بررسی میکنیم.
tan (تانژانت): نسبت طول ضلع مقابل به طول ضلع مجاور.
cot (کتانژانت): نسبت طول ضلع مجاور به طول ضلع مقابل.
sin (سینوس): نسبت طول ضلع مقابل به طول وتر.
cos (کسینوس): نسبت طول ضلع مجاور به طول وتر.
شاید در ابتدا این تعاریف برای شما نامفهوم باشد و کمی سردرگم شوید. ولی نگران نباشید، با توجه به شکل مثلث قائمالزاویه زیر تمامی سوالات ذهن شما پاسخ داده خواهد شد. در ابتدا یک مثلث قائمالزاویه در نظر بگیرید و اندازه یکی از زاویهها را برابر α فرض خواهیم کرد.
اکنون میخواهیم با حل یک مثال ساده نسبتهای مثلثاتی زاویههای 30، 45، 60 درجه را بدست آوریم. با توجه به مثلثهای قائمالزاویه شکل زیر و با کمک تعاریف نسبتهای مثلثاتی، این نسبتها را برای زوایای 30، 45، 60 درجه بدست آورید.

اکنون با توجه به تعاریف نسبتهای مثلثاتی، این مقادیر را برای زاویههای 30، 45 و 60 درجه در جدول زیر خواهیم نوشت:
| 60 | 45 | 30 | مقدار |
| 2 / 3√ | 2 / 2√ | 2 / 1 | sin |
| 2 / 1 | 2 / 2√ | 2 / 3√ | cos |
| 3√ | 1 | 3 / 3√ | tan |
| 3 / 3√ | 1 | 3√ | cot |
اکنون میخواهیم به کمک نسبتهای مثلثاتی، فرمولی برای مساحت یک مثلث بیابیم. همانطور که میدانید، مساحت هر مثلث برابر است با: ارتفاع × قاعده × 1/2.
اکنون مثلث ABC را در نظر میگیریم و با توجه به فرمول مساحت رابطه جدیدی برای آن خواهیم یافت:
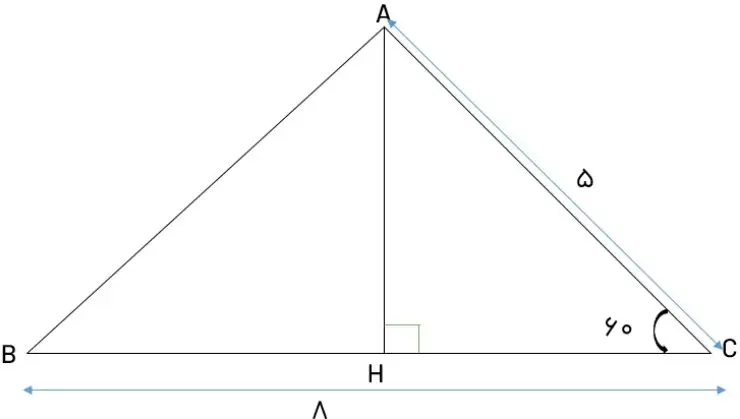
از فرمول قبلی مساحت داریم: (AH × BC) × 1/2 . حال اگر دقت کنیم، ارتفاع AH در واقع ضلع مقابل به وتر در مثلث AHC میباشد. یعنی میتوانیم به جای AH، مقدار sin60 × AC را جایگذاری کنیم. پس بدین ترتیب مساحت مثلث برابر است با: (AC × BC × sinC) × 1/2
یعنی در یک مثلث با داشتن مقادیر دو ضلع مثلث و زاویه بین آنها میتوانیم مساحت را محاسبه کنیم.
آموزش فصل دوم ریاضی دهم تجربی دایره مثلثاتی
دایره مثلثاتی یکی از مباحث جذابی است که در آموزش فصل دو ریاضی دهم به طور کامل مورد بررسی قرار میدهیم. یک دایره همانند شکل زیر در نظر بگیرید که دو زاویه در آن قرار دارد. میخواهیم مشخص کنیم که کدام یک از زاویهها مثبت و کدام یک منفی است. برای این کار همیشه این نکته را به خاطر بسپارید که اگر در جهت عقربههای ساعت حرکت کنیم، زاویه منفی و اگر در خلاف جهت عقربههای ساعت حرکت کنیم، زاویه مثبت است.
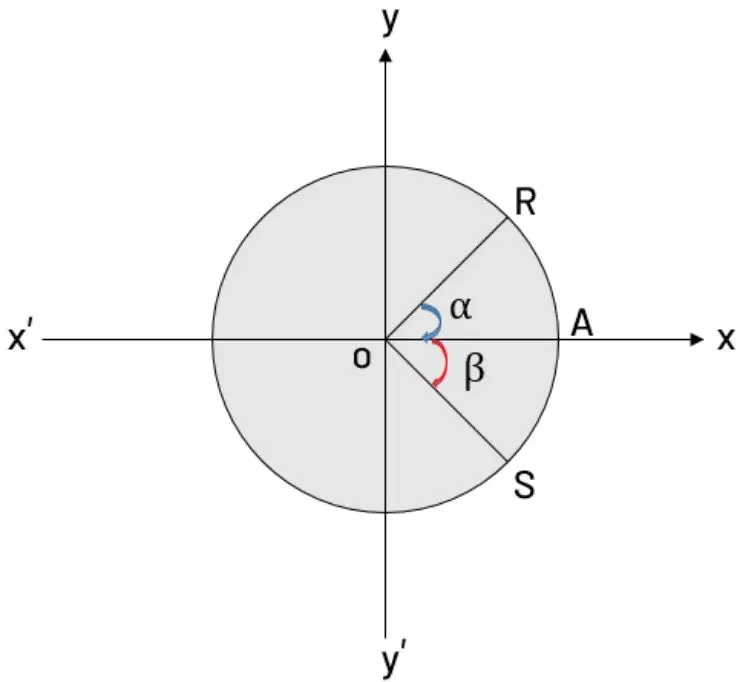
در نتیجه با توجه به نکته قبلی میتوانیم بگوییم زاویه α، مثبت و زاویه β، منفی است.
نواحی مختلف دایره مثلثاتی
دایره مثلثاتی به چهار ربع تقسیم میشود. در دایره مثلثاتی از مبدا تا زاویه 90 درجه را ربع اول میگویند. همچنین از 90 درجه تا 180 را ربع دوم مینامند. ربع سوم دایره مثلثاتی از 180 درجه تا 270 درجه را شامل میشود. ربع چهارم نیز ناحیه بین 270 درجه تا 360 درجه است. پس بازه یک دایره مثلثاتی از 0 تا 360 درجه میباشد. همانطور که قبلا اشاره کردیم با حرکت در خلاف جهت عقربههای ساعت زاویه مثبت و با حرکت در جهت عقربههای ساعت زاویه منفی است. نواحی مختلف یک دایره مثلثاتی را در شکل زیر مشاهده میکنید.
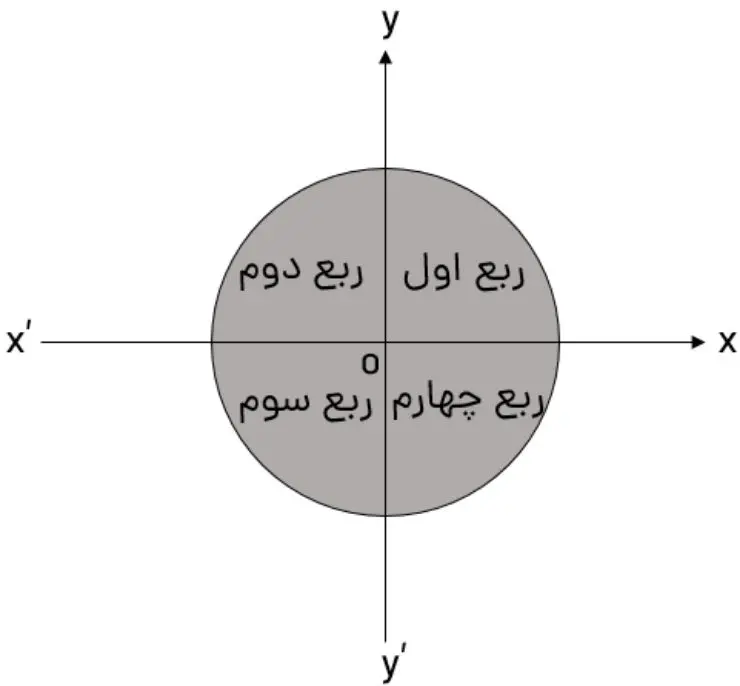
نکته: زاویههای 0، 90، 180، 270، 360 را در هیچ کدام از نواحی فوق درنظر نمیگیریم چون این زوایا، زاویههای مرزی هستند.
نسبتهای مثلثاتی زوایای مرزی
در این بخش از آموزش فصل دو ریاضی دهم به بررسی نسبتهای مثلثاتی زوایای مرزی میپردازیم. قبلا اشاره کردیم که زوایای 0، 90، 180، 270 و 360 درجه زوایای مرزی هستند. اکنون به کمک دایره مثلثاتی زیر تمامی نسبتهای مثلثاتی این زوایا را بدست میآوریم.
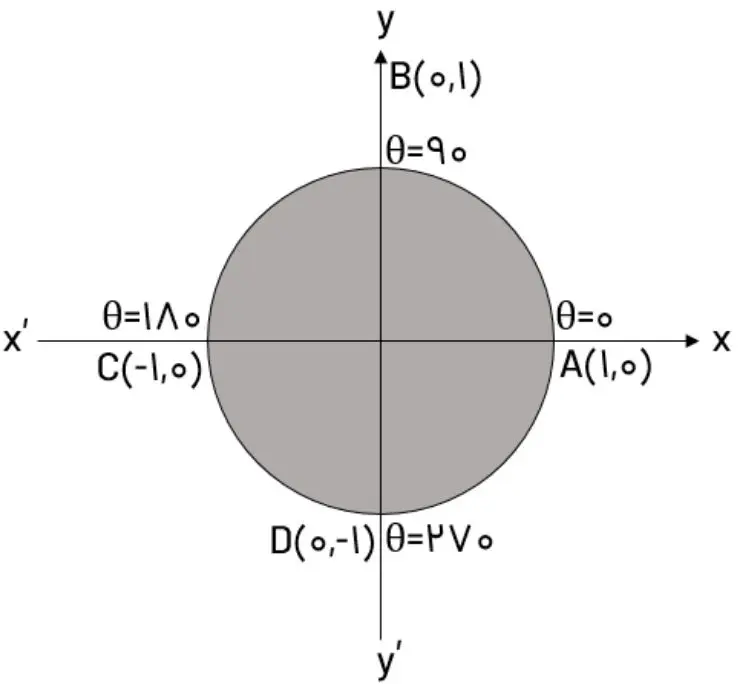
خب با توجه به تعاریفی که از نسبتهای مثلثاتی در بخش قبل بیان کردیم، در جدول زیر این نسبتها را برای زوایای مرزی خواهیم نوشت.
| 360 | 270 | 180 | 90 | 0 | مقدار |
| 0 | 1- | 0 | 1 | 0 | sin |
| 1 | 0 | 1- | 0 | 1 | cos |
| 0 | تعریف نشده | 0 | تعریف نشده | 0 | tan |
| تعریف نشده | 0 | تعریف نشده | 0 | تعریف نشده | cot |
اکنون در گام بعدی میخواهیم نسبتهای مثلثاتی را برای نواحی چهارگانه تعیین میکنیم. یعنی میخواهیم بدانیم که مقادیر محتلف در هر ناحیه مثبت است یا منفی؟ جدول زیر یکی از مهمترین جداول این فصل است که با کمک آن بسیاری از سوالات این فصل را حل خواهیم کرد. پس با دقت سعی کنید مطالب این جدول را به خاطر بسپارید.
| ربع چهارم | ربع سوم | ربع دوم | ربع اول | مقدار |
| – | – | + | + | sinθ |
| + | – | – | + | cosθ |
| – | + | – | + | tanθ |
| – | + | – | + | cotθ |
از جدول فوق یک نکته بسیار مهم دیگر نیز بدست میآید:
نکته: برای هر زاویه دلخواه مقدار sin و cos بین دو عدد 1 و 1- خواهد بود. یعنی برای هر زاویهای مقادیر sin و cos از 1 بیشتر و از 1- کمتر نخواهد بود.
رابطه شیب خط با تانژانت زاویه
یکی از کاربردهای نسبتهای مثلثاتی در بدست آوردن شیب یک خط میباشد. برای درک بهتر این موضوع با هم به بررسی یک مثال خواهیم پرداخت. نمودار خط 6 – y = 3x در شکل زیر رسم شده است. دو نقطه به مختصات B=(4,6) و A=(5,9) روی این خط در نظر بگیرید و از هر دو نقطه عمودی بر محور xها رسم کنید. شیب این خط و تانژانت زاویه مشخص شده را بدست آورده و با هم مقایسه کنید.
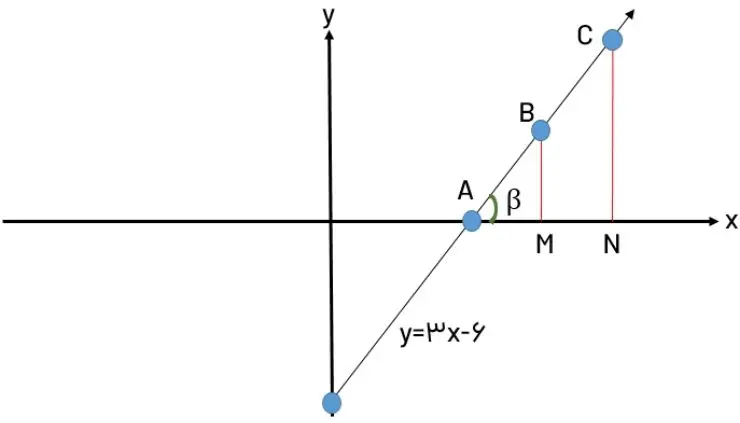
خب دوستان عزیز پایه هفتم شما در مثال از ما خواسته شده که شیب این خط و تانژانت زاویه β را بدست آوریم. شما به خوبی میدانید که شیب یک خط برابر است با مقدار تفاضل عرضها تقسیم بر مقدار تفاضل طولها. تانژانت یک زاویه نیز برابر است با ضلع مقابل به وتر تقسیم بر ضلع مجاور به وتر. پس با توجه به تعاریف خواهیم داشت:
3 = (4 – 5) ÷ (6 – 9) = شیب خط ، 3 = 2 ÷ 6 = (2 – 4) ÷ (0 – 6) = (BM ÷ AM) = tanβ
از مثال فوق نتیجه میگیریم: شیب هر خط که محور افقی را قطع کند، برابر است با تانژانت زاویه بین آن خط و جهت مثبت محور افقی. به عبارت دیگر، اگر β زاویهای باشد که خط با جهت مثبت محور افقی میسازد، آنگاه: tanβ = شیب خط
ریاضی دهم تجربی فصل دوم روابط بین نسبتهای مثلثاتی
در آخرین مبحث از آموزش فصل دو ریاضی دهم به سراغ روابط بین نسبتهای مثلثاتی خواهیم رفت. پیش از این شما را با نسبتهای مثلثاتی و دایره مثلثاتی آشنا کردیم. برای یادگیری روابط بین نسبتهای مثلثاتی شما باید مباحث قبل را به خوبی یاد گرفته باشید. پس توصیه میکنم در صورت وجود مشکل در مباحث پیشین یک بار دیگر آموزش این مباحث را مطالعه کنید و سپس به سراغ روابط بین نسبتهای مثلثاتی بیابید.
اولین رابطه را به کمک یک مثال توضیح خواهیم داد. مثلث قائمالزاویه زیر را در نظر بگیرید و با توجه به این شکل نسبتهای مثلثاتی را برای زاویه θ بیابید. همچنین مقدار Sin2θ + cos2 θ را نیز محاسبه کنید.
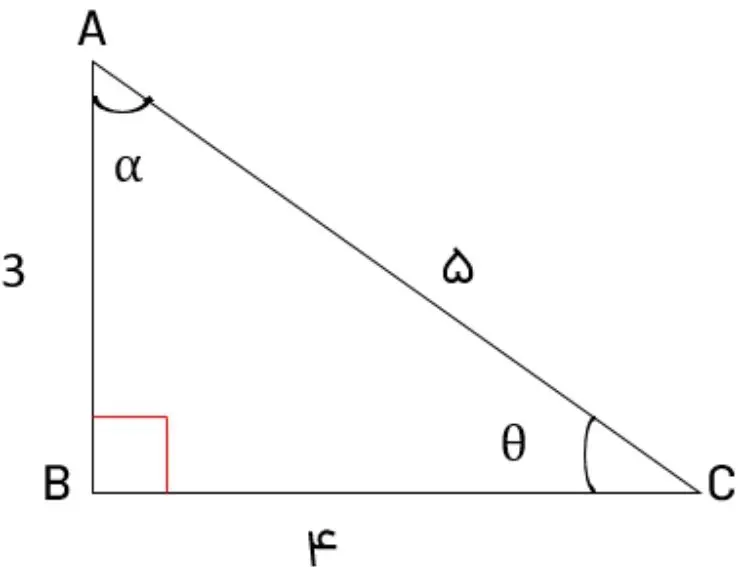
با توجه به شکل فوق مقادیر خواسته شده در صورت سوال برابر است با:
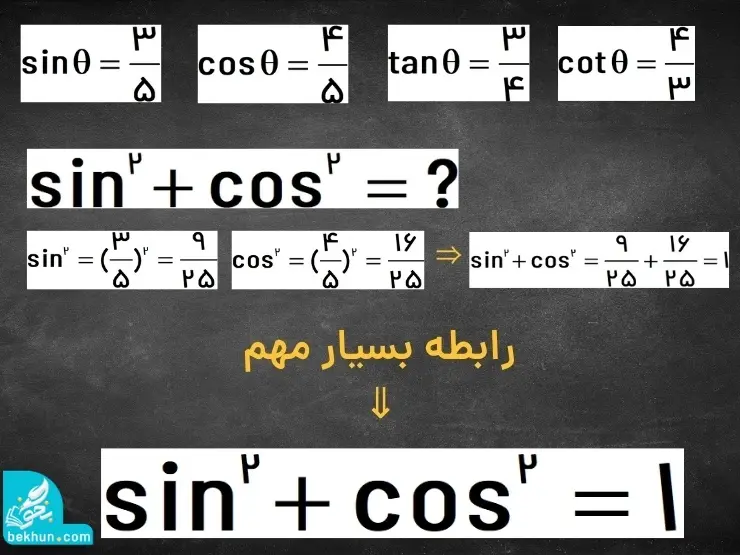
رابطه فوق یکی از مهمترین روابط مثلثاتی است که برای تمام زاویهها برقرار است. همچنین از این رابطه میتوانیم به روابط مهم دیگر نیز دست پیدا کنیم. در ادامه از همین رابطه دو رابطه مهم دیگر برای sin و cos یک زاویه بدست خواهیم آورد.
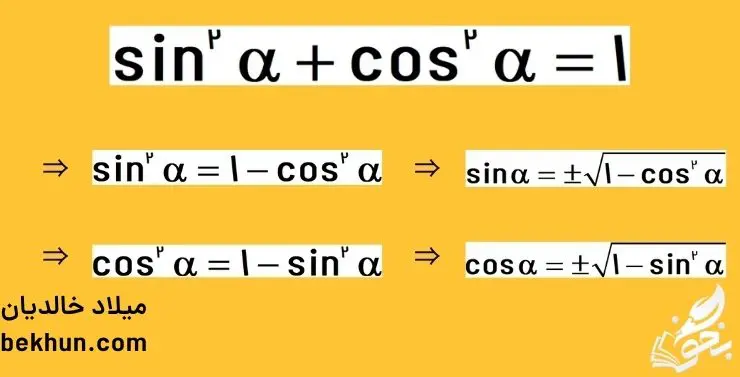
علامت مثبت و منفی در روابط بالا با توجه به ناحیهای که زاویه α در آن قرار دارد، مشخص میشود.
رابطههای تانژانت بر حسب کسینوس و کتانژانت بر حسب سینوس
در قسمت قبل از آموزش فصل دو ریاضی دهم، روابطی برای سینوس و کسینوس معرفی کردیم. حال میخواهیم به کمک همان روابط، برای تانژانت و کتانژانت یک زاویه به رابطه مهمی برسیم. این روابط بسیار در حل تمرینات و سوالات این فصل کاربرد دارد.
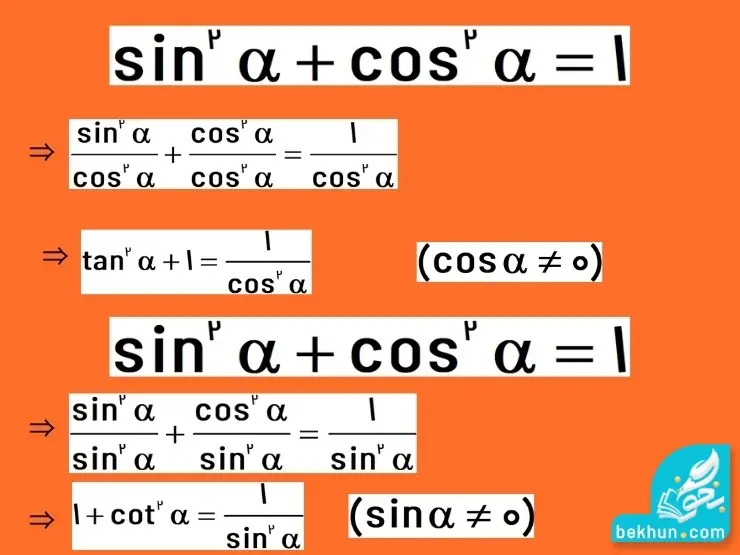
اتحاد مثلثاتی
هر یک از رابطههایی که بدست آوردیم و به ازای هر α برقرار است را یک اتحاد مثلثاتی مینامیم. حال این سوال پیش میآید که یک عبارت را چه وقت یک اتحاد مثلثاتی مینامیم؟ هرگاه بتوانیم از یک طرف تساوی به کمک روابط مثلثاتی به طرف دیگر تساوی برسیم، یک تساوی(اتحاد) بین دو عبارت مثلثاتی برقرار خواهد بود. برای درک بهتر این موضوع میخواهیم یک مثال بررسی کنیم.
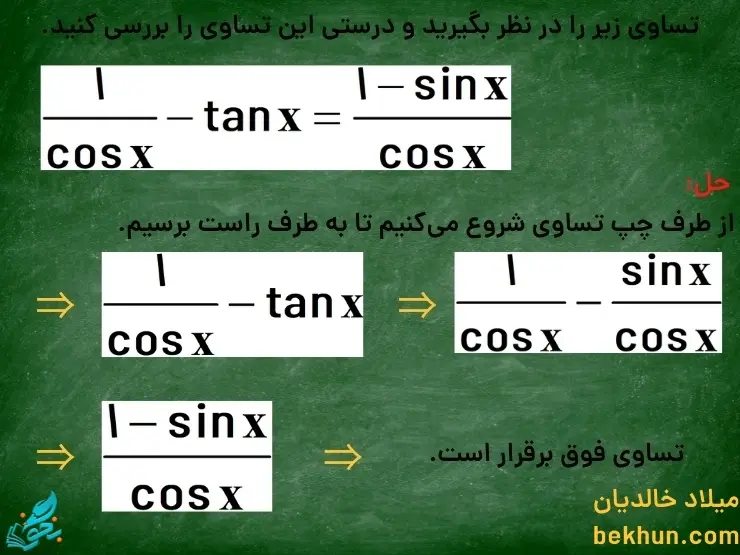
همانطور که در مثال فوق مشخص شد به کمک یک رابطه ساده مثلثاتی توانستیم اتحاد مثلثاتی فوق را اثبات کنیم.
در آخرین بخش از مقاله آموزش فصل دو ریاضی دهم روابط مثلثاتی که بدست آوردیم را جمعبندی میکنیم تا شما عزیزان این روابط را به آسانی در اختیار داشته باشید.

کلام پایانی
دوستان عزیز پایه دهم به پایان مقاله آموزش فصل دو ریاضی دهم رسیدیم. یادگیری و تسلط بر مطالب این فصل با مقالات گام به گام فصل دو ریاضی دهم و نمونه سوال فصل دو ریاضی دهم تکمیل خواهد شد. شما عزیزان میتوانید با کلیک بر روی لینک آموزش فصل اول ریاضی دهم، از این مقاله برای یادگیری مطالب فصل اول استفاده کنید. همچنین از طریق آموزش ریاضی دهم به تمامی مقالات آموزشی برای فصلهای کتاب درسی دسترسی خواهید داشت. در ضمن با لینک ریاضی دهم همه مقالات مرتبط با ریاضی پایه دهم به صورت کاملا رایگان دریافت کنید. تمامی مقالات دروس مختلف پایه دهم را با کلیک بر روی لینک دهم مشاهده کنید.
در پایان از شما دعوت میکنم با عضویت در سایت بخون بهترین مقالات آموزشی را به صورت کاملا رایگان مطالعه کنید. همچنین در صورت رضایت از مقاله آموزش فصل دو ریاضی دهم این مقاله را با دوستان خود به اشتراک بگذارید. در ضمن با ثبت نظرات خود باعث پیشرفت ما در نوشتن بهتر و مفیدتر مقالات شوید و با ثبت ستارههای رنگی باعث دلگرمی و انگیزه ما در نوشتن مقالات شوید.
راستی اگر دوست دارید از نمونه سوالات رایگان ما در سایت بخون هم استفاده کنید میتوانید با کمک لینکهای زیر به نمونه سوالات ریاضی دهم که از یک بانک سوال استاندارد تشکیل شده دسترسی داشته باشید:
- نمونه سوال ریاضی دهم رشته ریاضی نوبت دوم
- نمونه سوال فصل مثلثات ریاضی دهم با جواب
- نمونه سوال ریاضی دهم انسانی نوبت دوم
- نمونه سوال هندسه دهم نوبت دوم با جواب
- حل تمرینات ریاضی دهم تجربی
سوالات متداول
- آیا در مقاله آموزش فصل دو ریاضی دهم مطالب کتاب درسی به طور کامل بررسی شده است؟
بله، در این مقاله تمامی مباحث کتاب درسی با زبانی ساده بیان شده است. - آیا در مقاله آموزش فصل دو ریاضی دهم تمرینات کتاب درسی نیز حل شده است؟
خیر، برای حل سوالات کتاب درسی از مقاله گام به گام فصل دو ریاضی دهم استفاده کنید. - آیا در این مقاله نمونه سوالات امتحانی نیز برای فصل دو ریاضی دهم حل شده است؟
خیر، برای حل سوالات امتحانی از مقاله نمونه سوال فصل دو ریاضی دهم کمک بگیرید.






