امروز در سایت بخون با آموزش فصل اول ریاضی دهم در خدمت شما عزیزان هستیم. درس ریاضی از جمله درسهایی است که برای تسلط در آن باید یک منبع خوب آموزشی در اختیار داشته باشید. پس از یادگیری نیز باید با حل تمرینات مختلف مهارت خود را به بالاترین حد ممکن برسانید. حتما الان از خود میپرسید: “از کجا منبعی پیدا کنم که هم خوب آموزش داده باشه و هم تمرینات خوبی داشته باشه”؟
باید به شما این مژده را بدهم که در این مقاله بهترین آموزش فصل اول ریاضی دهم را در اختیارتان میگذاریم. همچنین در مقالات بعدی تمرینات و تستهای فوقالعادهای براتون میاریم تا خیال شما را برای بیست گرفتن در درس ریاضی راحت کنیم. پس اگر میخواهید به بهترین نمره برسید و بتوانید تستهای کنکور فصل اول ریاضی دهم را مثل آب خوردن حل کنید، تا انتهای این مقاله را مطالعه فرمایید.
در ابتدای آموزش فصل اول ریاضی دهم با مباحثی که در این فصل مطرح میشود، آشنا خواهیم شد. سپس هر کدام از این مباحث را به کاملترین شکل مورد بررسی قرار خواهیم داد. مباحثی که در فصل اول ریاضی دهم مطرح میشود، عبارتند از:

نکته قابل توجه این است که از فصل اول ریاضی دهم در کنکور سراسری سوال مطرح میشود. پس به نحوی به شما آموزش میدهیم که بتوانید علاوه بر سوالات تشریحی به سوالات تستی مطرح شده در کنکور نیز پاسخ دهید. حالا وقت اون رسیده که با تمام تمرکز خود با ما همراه شوید و قدم به قدم مطالب فصل اول ریاضی دهم را یاد بگیرید. در ضمن آموزش سایر فصلهای ریاضی دهم را هم از طریق بخش آموزش ریاضی دهم مشاهده کنید که به شدت میتواند به شما کمک کند.
مجموعه متناهی و نامتناهی ریاضی دهم
خب مبحث مجموعههای متناهی و نامتناهی را با یادآوری مجموعههایی که قبلا آموختهایم، شروع میکنیم. در پایههای پایینتر با مجموعههای زیر آشنا شدیم:

اگر کمی دقت کنید به این نتیجه میرسید که تمامی مجموعهها زیر مجموعه اعداد حقیقی هستند. این نکته مهم را با دیدن شکل زیر بخاطر بسپارید.

از شکل فوق رابطهای بدست میآید که به صورت مقابل است: N ⊆ W⊆ Z ⊆ Q ⊆ R. خب حالا که مجموعه اعداد مختلف را با هم مرور کردیم، به سراغ مبحث بازهها میرویم. اما اگر دقت کنید در کتاب درسی تمریناتی که وجود دارد از اهمیت بالایی برخوردار هستند؛ اما یک خبر خوب هم برای شما داریم، در بخش گام به گام ریاضی دهم، برای تمامی فصل ها پاسخ تمامی سوالات کتاب درسی را به صورت رایگان تنظیم کرده و در اختیار شما عزیزان قرار داده ایم.
آموزش بازهها ریاضی دهم
یکی از مباحث مهم در بحث مجموعهها، مبحث بازهها میباشد. ابتدا با مفهوم بازه آشنا میشویم و سپس انواع بازه را با هم بررسی میکنیم. همانطور که اشاره کردیم تمامی مجموعهها، زیر مجموعه اعداد حقیقی هستند. اکنون زیر مجموعه کوچکی از اعداد حقیقی را در نظر میگیریم. فرض کنید مجموعه N شامل تمام اعداد حقیقی بین 1- و 2 باشد. نمایش ریاضی این مجموعه به صورت مقابل است: N={x∈R | -1≤x≤2 }. این زیر مجموعه به یک قطعه مشخص از اعداد حقیقی اشاره میکند، که به آن بازه یا فاصله میگوییم.
حال میخواهیم انواع مختلف بازهها را به سادهترین زبان بیان کنیم:
الف) بازه بسته: اگر بازه شامل هر دو نقطه انتهایی خود باشد، آن را بازه بسته مینامند. این بازه را به صورت [1,2-] نشان میدهیم.
ب) بازه نیم باز: اگر بازه شامل یکی از نقاط انتهایی خود باشد، آن را بازه نیم باز مینامند. این بازه را به صورت [1,2-} یا {1,2-] نشان میدهیم.
ج) بازه باز: اگر بازه شامل هیچ یک از نقاط ابتدایی و انتهایی خود نباشد، آن را بازه باز مینامند. این بازه را به صورت {1,2-} نشان میدهیم.
اکنون برای یادگیری بهتر مبحث بازهها یک تمرین انجام میدهیم.(سعی کنید تمرینات را ابتدا خودتان حل کرده و سپس پاسخ را مقایسه کنید).
| نمایش هندسی | نمایش مجموعهای | بازه | نوع بازه |
| [m,n} | نیم باز | ||
 |
{x∈R | m ≤ x ≤ n} | بسته | |
| باز | |||
| [m,n] | بسته | ||
| {x∈R | m ≤ x < n} | |||
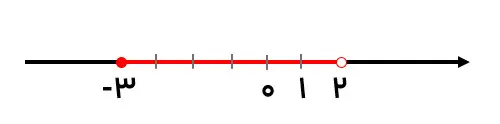 |
برای حل این مثال باید به این نکات توجه داشته باشیم: علامتهای } و < برای قسمت باز به کار میرود و علامتهای [ و ≤ برای قسمت بسته کاربرد دارد. همچنین در بخش نمایش هندسی دایره توپر نشاندهنده بازه بسته و دایره توخالی نشاندهنده بازه باز میباشد.
آشنایی با مثبت و منفی بینهایت
چگونه برای معادله 3n<6 جوابی به شکل بازه تعیین کنیم؟ اگر این نامعادله را حل کنیم به جواب مقابل میرسیم: n<2 یا به شکل مجموعهای {x∈R | x < 2}. همانطور که مشاهده میکنید مجموعه فوق نامتناهی است.(در ادامه مجموعههای متناهی و نامتناهی را توضیح خواهیم داد). نمایش بازهای این مجموعه به صورت مقابل میباشد: (2,∞-). اگر معادله به شکل 3n>6 باشد، آنگاه جواب ما به چه صورتی خواهد بود؟
اجتماع و اشتراک مجموعهها
مبحث اجتماع و اشتراک را میخواهیم با یک مثال ساده یاد بگیریم. دو مجموعه زیر را در نظر بگیرید و به اجتماع و اشتراک این دو مجموعه را بیابید.
M=(-2,3] , N=(1,+∞) M∪N=? , M∩N=?
هر دو مجموعه را در نمودار زیر رسم کردهایم: 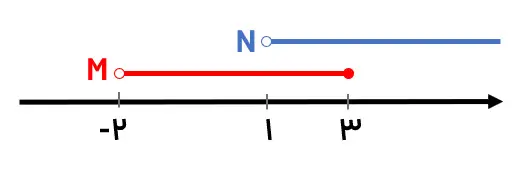
با توجه به شکل مشخص است که M∪N برابر است با مجموعه اعداد حقیقی بزرگتر از (2-). همچنین M∩N برابر است با مجموعه اعداد حقیقی بین 1 و 3 که شامل خود عدد 3 هم میشود، یعنی:
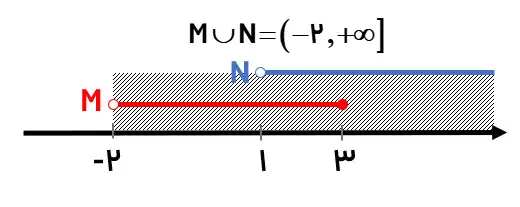
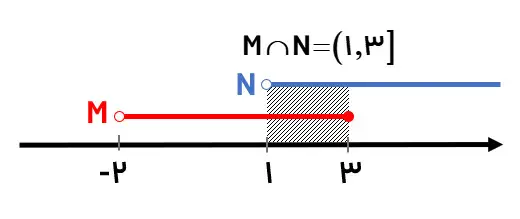
نکات کلیدی در اجتماع و اشتراک: در اینجا میخواهیم با دو نکته کلیدی تمام سوالات اجتماع و اشتراک را در کمتر از یک دقیقه حل کنیم:
- برای اجتماع کوچکترین عضو بازه کوچکتر و بزرگترین عضو بازه بزرگتر را پیدا میکنیم و با علامت قبل از آن مینویسیم.
- برای اشتراک بزرگترین عضو بازه کوچکتر و کوچکترین عضو بازه بزرگتر را مییابیم و با علامت قبل از آن مینویسیم.
برای مثال بالا کوچکترین عضو بازه کوچکتر 2- است و بزرگترین عضو بازه بزرگتر ∞+ است پس اجتماع میشود: بازه باز 2- تا ∞+. در مورد اشتراک هم بزرگترین عضو بازه کوچکتر 3 است و کوچکترین عضو باز بزرگتر 1 است، پس اشتراک میشود: بازه باز 1 تا 3 بسته.
مجموعه متناهی و نامتناهی
در اینجا شما را با سادهترین تعریف مجموعه متناهی و نامتناهی آشنا میکنیم: مجموعهای که هر دو طرف بازه آن عدد باشد را مجموعه متناهی مینامند. مجموعهای که یک طرف آن ∞+ یا ∞- باشد را مجموعه نامتناهی مینامند(به همین سادگی و خوشمزگی!!!). حال با این تعاریف متناهی و نامتناهی بودن مجموعههای زیر را مشخص کنید.
A=(1,5) , B=(-∞,5) , C=[-10,+∞) , D= مجموعه اعداد مثبت کوچکتر از 4 , E= مجموعه اعداد بزرگتر از منفی 6
ریاضی دهم تجربی فصل اول | مبحث متمم یک مجموعه
در ادامه آموزش فصل اول ریاضی دهم به مبحث متمم یک مجموعه میرسیم. برای یادگیری مبحث متمم یک مجموعه ابتدا با مجموعه مرجع آشنا میشویم. در هر موضوعی، مجموعهای که سایر مجموعهها زیر مجموعه آن هستند را مجموعه مرجع مینامند و آن را با علامت U نشان میدهند. اگر مجموعه N زیر مجموعه، مجموعه مرجع باشد آنگاه مجموعه U – N را مجموعه متمم N نامیده و با علامت `N نشان میدهیم. با یک مثال این موضوع را بهتر توضیح میدهیم: مجموعه اعداد اول یک رقمی = A و مجموعه اعداد یک رقمی = U. میخواهیم متمم A را بیابیم، پس:
U={1,2,….,9} , A={2,3,5,7} ⇒ A`= U – A ={1,4,6,8,9}
حال که با متمم یک مجموعه آشنا شدید با ارائه یک مثال ساده به نکات جالبی درباره متمم یک مجموعه میرسیم. مجموعههای A و B و U را در نظر بگیرید:
U={1,2,….9} , A={1,2,3,6} , B={7,9}. متمم های A , B را محاسبه میکنیم و حاصل سایر عبارات خواسته شده را بدست میآوریم:
A`={1,4,5,7,8,9} , B`={1,2,3,4,5,6,8}. حال حاصل عبارات زیر را بدست آورده و به نتایج مهمی خواهیم رسید.
(A`)`= , A ∪ B= , (A ∪ B)`= , A`∩ B`= , A ∩ B= , (A ∩ B)`= , A` ∪ B`= , A – B = , A – ( A ∩ B)= , A ∩ B`=
اگر حاصل عبارات فوق را بدست بیاوریم به نتایج زیر خواهیم رسید:
متمم، متمم هر مجموعهای برابر با خود آن مجموعه است.
A`∩ B`= (A ∪ B)` و (A ∩ B)`= A` ∪ B` و A – ( A ∩ B)= A ∩ B`
به دو مجموعه که فاقد عضو مشترک باشند، دو مجموعه جدا از هم میگویند.(آیا در مثال فوق دو مجموعه A , B ، دو مجموعه جدا از هم هستند؟).
تعداد عضوهای اجتماع دو مجموعه
در اینجا میخواهیم یک رابطه بسیار مهم و کاربردی را بررسی کنیم. برای نشان دادن تعداد اعضای یک مجموعه از نماد (نام مجموعه)n استفاده میکنیم. حال میخواهیم با بررسی یک مثال ساده به یک رابطه ریاضی برای n(A∪ B) برسیم.
فرض کنید در یک کلاس 10 نفر به رشته ریاضی و 15 نفر به رشته تجربی علاقه مند هستند. همچنین 5 نفر به هر دو رشته علاقه دارند. تعداد دانشآموزان این کلاس چند نفر است؟ برای پاسخ به این سوال موارد بصورت زیر عمل میکنیم:
A= تعداد دانشآموزان علاقهمند به رشته ریاضی , B= تعداد دانشآموزان علاقهمند به رشته تجربی , A∩B= علاقهمند به هر دو رشته , A∪B= کل دانشآموزان
n(A)=10 , n(B)=15 , n(A∩B)=5 ⇒ n(A ∪ B)=? : حال به شکل زیر دقت کنید
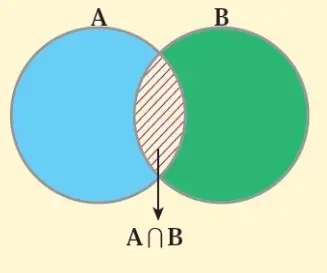
همانطور که از شکل مشخص است برای بدست آوردن تعداد کل دانشآموزان باید مجموع تعداد علاقهمندان به رشته ریاضی و تجربی را بدست آوریم و سپس حاصل را از تعدادی که به هر دو رشته علاقه دارند، کم کنیم. به زبان ریاضی داریم:
n(A ∪ B)= n(A) + n(B) – n(A∩B) ⇒ n(A ∪ B)= 10 + 15 – 5 = 20
فرمول بسیار مهم: n(A ∪ B)= n(A) + n(B) – n(A∩B)
فصل اول ریاضی دهم تجربی | مبحث الگو و دنباله
مبحث الگو و دنباله سومین مبحثی است که در آموزش فصل اول ریاضی دهم به آن میپردازیم. شما در سالهای قبل نیز با الگوسازی آشنا شدهاید. حتی اگر این مبحث را قبلا خوب یاد نگرفتهاید، نگران نباشید چون ما آنچه از الگوسازی و دنباله که نیاز باشد را به شما یاد خواهیم داد. یافتن رابطه و الگو میان اعداد همیشه لذتبخش است. با هم به الگو زیر توجه کنیم و رابطه آن را بیابیم:
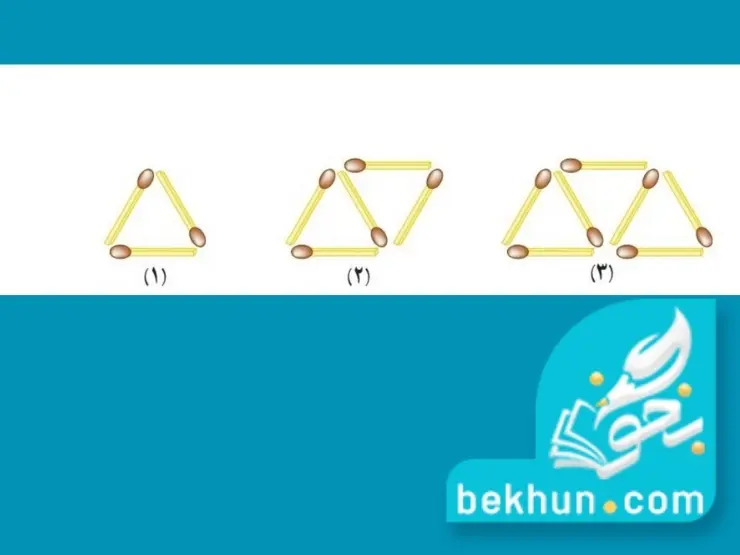
| n | 5 | 4 | 3 | 2 | 1 | n= شماره شکل |
| 2n+1 | 11 | 9 | 7 | 5 | 3 | an= تعداد چوب کبریت |
به الگوهایی همانند مثال فوق که فاصله بین جملات آن یکسان است، الگوهای خطی میگویند. شکل کلی الگوهای خطی به صورت tn =an+b میباشد. هر الگویی که رابطه آن به شکل فوق نباشد را الگو غیر خطی میگویند. مثالی از یک الگو غیر خطی را در شکل زیر مشاهده میکنید:
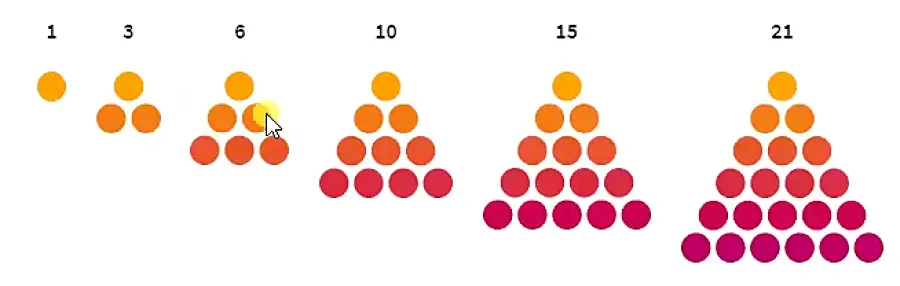
الگو شکل فوق را بیابید و جواب خود را از قسمت نظرات برای ما ارسال کنید.
دنباله
هر تعداد عدد که پشت سر هم بیایند، یک دنباله را تشکیل میدهند. هر کدام از این اعداد یک جمله از دنباله را تشکیل میدهند. هر دنبالهای دارای یک جمله عمومی است. به کمک جمله عمومی میتوانیم هر یک از جملات دنباله را بیابیم. چند نمونه از جملههای عمومی یک دنباله را در ادامه برای شما نوشتهایم. سعی کنید چند جمله از هر کدام از این دنبالهها را بنویسید.
الف) an = 3n+4 ب) an = n2 ج)an = n2 + 3
دنباله (الف) از درجه یک و دنبالههای (ب) و (ج) از درجه دو هستند. درجه دنباله با توجه به جمله عمومی دنباله تعیین میشود.
آموزش فصل اول ریاضی دهم رشته ریاضی | مبحث دنبالههای حسابی و هندسی
بالاخره به مهمترین مبحث در آموزش فصل اول ریاضی دهم رسیدیم. مبحث دنبالههای حسابی و هندسی همواره مورد توجه طراحان کنکور سراسری بوده است. شما در طول این فصل با تعریف دنباله و دنبالههای خطی و غیر خطی آشنا شدید. اکنون میخواهیم شما را با دنبالههای حسابی و هندسی آشنا کنیم. پس ذهن خود را آماده کنید و با تمام تمرکز به ادامه این مطلب توجه کنید.
دنباله حسابی
به دنبالهای که هر جمله آن از جمع جمله قبلی با مقداری ثابت بدست میآید، دنباله حسابی میگویند. این مقدار ثابت را قدر نسبت دنباله حسابی مینامند و با حرف d نمایش میدهند. میخواهیم یک مثال جذاب از دنباله حسابی برای شما بیاوریم. جام جهانی فوتبال هر چهار سال یک بار برگزار میشود. دنباله مربوط به آن را از سال 1998 شروع میکنیم و به کمک شما سایر جملات را مشخص میکنیم.
1998 , 2002 , 2006 , 2010 ,…….. a1 =? d=?
واضح است که جمله اول دنباله فوق 1998 است و قدر نسبت این دنباله هم 4 میباشد. اگر بخواهیم یک رابطه کلی برای قدر نسبت و جمله عمومی یک دنباله حسابی بنویسیم، خواهیم داشت: d=an – an-1 و an = a1 + (n – 1)d
چند دنباله برای شما آوردهایم، سعی کنید جملات عمومی این دنبالهها را بدست آورید.
الف)……، 19، 14، 9 ب)…..، 13، 9، 6 ج)…..، 23، 16، 9
دنباله هندسی
به دنبالهای که هر جمله آن (به جز جمله اول) از ضرب جمله قبلی در عددی ثابت و غیر از صفر بدست آید را دنباله هندسی میگویند. این عدد ثابت را قدرنسبت دنباله هندسی میگویند. نکته مهم در دنباله هندسی این است که جمله اول این دنباله نمیتواند صفر باشد. به دنباله هندسی زیر توجه کنید:
5 , 10 , 20 , …….. a1 =? r=?
خب جمله اول دنباله فوق که 5 است و قدر نسبت این دنباله 2 میباشد. همانند دنباله حسابی برای جمله عمومی و قدر نسبت دنباله هندسی نیز رابطه کلی بین میکنیم که به صورت مقابل است: r= an / an – 1 و an = a1 rn-1
جملات عمومی دنبالههای هندسی که در زیر آورده شده را بیابید.
الف)…..,45 , 15 , 5 ب)……, 8, 4 , 2 , 1 ج)……, 28- , 14 , 7-
جمعبندی نهایی آموزش فصل اول ریاضی دهم
دانشآموزان دهمی و معلمهای عزیز به پایان آموزش فصل اول ریاضی دهم رسیدیم. در این فصل مطالب زیر را آموختیم:
- با بازهها و مجموعههای متناهی و نامتناهی آشنا شدیم.
- متمم یک مجموعه و فرمول کاربردی آن را یاد گرفتیم.
- با دنبالهها و الگوهای خطی و غیر خطی آشنا شدیم.
- دنبالههای حسابی و هندسی و جمله عمومی و قدر نسبت را آموختیم.
امیدوارم مطالب فصل اول ریاضی دهم را به خوبی یاد گرفته باشید. تمام تلاش بنده این است که شما در ابتدا به خوبی مطالب فصل اول ریاضی دهم را یاد بگیرید سپس با تمرین و تست به تسلط کامل برسید. اگر این مطلب در آموزش فصل اول ریاضی دهم مفید بوده آن را با دوستان خود به اشتراک بزارید. همچینین نظرات خود برای ما بنویسید که موجب ایجاد انگیزه و اشتیاق در ما خواهد شد. در ضمن برای تسلط کامل برروی مباحث این فصل حتما حتما از نمونه سوالات رایگانی که برای شما در بخش نمونه سوال ریاضی دهم قرار داده ایم استفاده کنید.
راستی اگر دوست دارید از نمونه سوالات رایگان ما در سایت بخون هم استفاده کنید میتوانید با کمک لینکهای زیر به نمونه سوالات ریاضی دهم که از یک بانک سوال استاندارد تشکیل شده دسترسی داشته باشید:
- نمونه سوال ریاضی دهم تجربی نوبت دوم با جواب
- نمونه سوال فصل دوم ریاضی دهم با جواب
- نمونه سوال ریاضی دهم انسانی نوبت دوم با جواب
- نمونه سوال ترم دوم هندسه دهم
- پاسخ تمرینات ریاضی دهم تجربی
سوالات متداول فصل اول ریاضی دهم
- فصل اول ریاضی دهم شامل چه مباحثی است؟
این فصل شامل مجموعههای متناهی و نامتناهی، متمم یک مجموعه، الگو و دنباله، دنبالههای حسابی و هندسی میباشد. - آیا در آموزش فصل اول ریاضی دهم کلیه مباحث بیان شده است؟
بله، کافیست وارد سایت شوید و مقاله را مطالعه کنید. - در کنکور سراسری چند سوال از فصل اول ریاضی دهم مطرح میشود؟
به طور میانگین 2 تا 3 سوال از این فصل طرح میشود. - آیا سایر فصلهای ریاضی با فصل اول ریاضی دهم ارتباط دارند؟
بله، فصل یک ریاضی دهم با سایر فصلها نیز ارتباط دارد.