سلام به همه رفقای پایه هفتمی عزیز و دوست داشتنی. امروز در سایت بخون می‌خواهیم با مقاله آموزش فصل اول ریاضی هفتم شما را شگفت‌زده کنیم!!! واقعیت این است که در دوره تحصیلی من اکثر دانش‌آموزان با ورود به یک مقطع تحصیلی بالاتر دچار افت درسی می‌شدند. این افت تحصیلی در درس ریاضی بیشتر از سایر دروس به چشم می‌آمد. اما شما اصلا نگران نباشید چون ما در اینجا هر آنچه برای موفقیت و پیشرفت درسی لازم باشد، در اختیارتان می‌گذاریم. خب همانطور که در کتاب درسی مشاهده می‌کنید فصل اول ریاضی هفتم در مورد راهبردهای حل مسئله است.
شاید شما نیز در درس ریاضی با مشکلاتی در حل مسائل رو به رو شده باشید و ناتوانی در حل مسئله موجب ناامیدی و دلسرذی هر دانش‌آموزی می‌شود. در این فصل 8 راهبرد برای حل مسائل مطرح شده است که هر کدام را به صورت کامل و دقیق بررسی خواهیم کرد. ابتدا با عنوان هر یک از این راهبردها آشنا شویم و سپس به سراغ بررسی هر راهبرد بپردازیم. راهبردهایی که در کتاب درسی برای حل مسئله آورده شده است عبارتند از:
- راهبرد رسم شکل
- راهبرد الگوسازی
- راهبرد حذف حالت‌های نامطلوب
- راهبرد الگویابی
- راهبرد حدس و آزمایش
- راهبرد زیرمسئله
- راهبرد حل مسئله ساده‌تر
- راهبرد روش‌های نمادین
در فصل اول ریاضی هفتم با مطلب جدیدی رو به رو نخواهید شد و همان مطالب دوره ابتدایی مرور خواهد شد. ما نیز در مقاله آموزش فصل اول ریاضی هفتم با تکنیک طرح سوال به آموزش مباحث خواهیم پرداخت. دوستان عزیز برای یادگیری کامل از شما می‌خواهم که با تمام تمرکز به مطالبی که در ادامه مقاله آموزش فصل اول ریاضی هفتم مطرح می‌شود، توجه کنید. من میلاد خالدیان هستم و به شما این اطمینان را می‌دهم که با این مقاله به راحتی آب خوردن در امتحانات مدرسه نمره 20 خواهید گرفت. پس کمتر از 10 دقیقه وقت بگذارید و این مقاله را تا انتها دنبال کنید.
راهبرد رسم شکل ریاضی هفتم
اولین قدم برای حل هر مسئله، فهمیدن مسئله است. یعنی شما باید بدانید که مسئله چه چیزی از شما می‌خواهد؟ سپس میتوانید برای مسئله خود راهبرد مناسب انتخاب کنید. با انتخاب راهبرد مناسب به راحتی میتوانید به حل مسئله بپردازید. مرحله آخر در حل مسئله، بازگشت به عقب است. یعنی بررسی کنید که جواب شما برای این مسئله درست و منطقی است یا خیر؟ پس به صورت خلاصه برای حل هر مسئله باید 4 مرحله زیر را انجام دهیم:
- فهمیدن مسئله
- انتخاب راهبرد مناسب
- حل مسئله
- بازگشت به عقب
خب حال که با مراحل حل هر مسئله آشنا شدیم به سراغ راهبردهای حل مسئله برویم. اولین راهبردی که مطرح می‌کنیم، راهبرد رسم شکل است. در بعضی مواقع با رسم شکل مسئله برای شما بسیار ساده می‌شود و تا حد زیادی حل می‌گردد. این راهبرد را با حل دو سوال مختبف بررسی می‌کنیم.
مثال 1) یک بازیکن بسکتبال را در نظر را بگیرید که توپی را از ارتفاع 24 متری رها می‌کند. توپ با هر بار برخورد با زمین نصف ارتفاع قبلی بالا می‌آید. پس از سه بار زمین خوردن، این توپ چند متر حرکت کرده است؟
حل: شاید در ابتدا حل این سوال مشکل به نظر بیاید اما در ادامه خواهید دید که با رسم شکل مناسب حل این سوال بسیار ساده است. به شکل زیر توجه کنید:
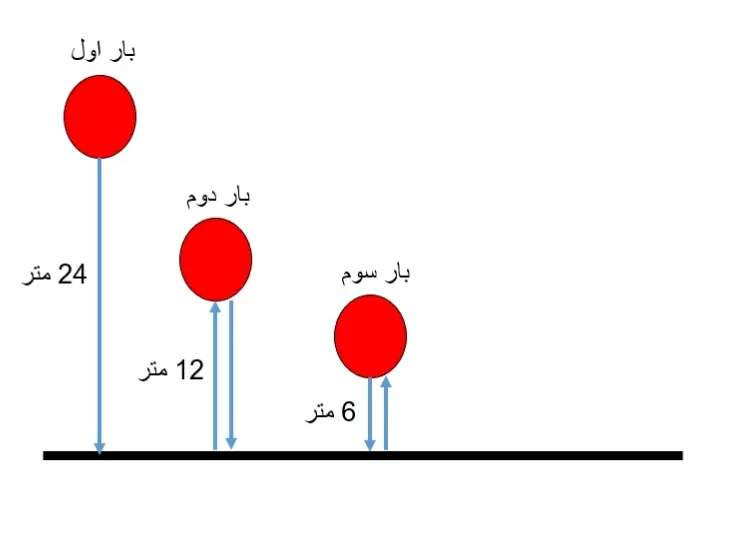
خب همانطور که در شکل مشخص است مسافتی که توپ طی کرده برابر است با: 60 = 6 + 6 + 12 + 12 + 24
پس یک سوال به ظاهر سخت و دشوار، با رسم یک شکل ساده به آسانی حل شد. بنابراین در اینجا بهترین راهبرد برای حل مسئله، راهبرد رسم شکل است. حال به سراغ یک مثال دیگر برویم:
مثال 2) مورچه‌ای را در نظر بکیرید که سعی دارد دانه گندمی را به بالای یک دیوار 10 متری ببرد. مورچه در هر بار بالا رفتن 3 متر بالا می‌رود و 1 متر به طرف پایین سر می‌خورد. این مورچه پس از چند بار بالا رفتن به بالای دیوار می‌رسد؟
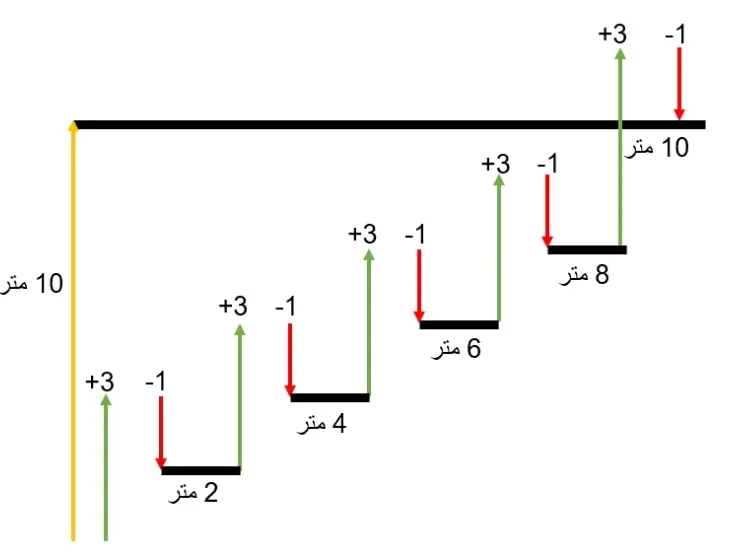با توجه به شکل بالا کاملا مشخص است که بعد از 5 مرحله مورچه به بالای دیوار می‌رسد.
آموزش ریاضی هفتم فصل اول راهبرد الگوسازی
دومین راهبردی که در آموزش فصل اول ریاضی هفتم با آن آشنا می‌شویم، راهبرد الگوسازی(تفکر نظام‌دار) است. گاهی در مسائل چندین حالت را برای رسیدن به جواب باید بررسی کنیم. حال این پرسش پیش می‌آید که چگونه هیچ حالتی را از قلم نیندازیم؟ برای اینکه اطمینان داشته باشید که تمامی حالات ممکن بررسی شده است از راهبرد الگوسازی استفاده کنید. در اینجا دو نمونه سوال برای یادگیری این راهبرد در برای شما آورده‌ایم تا به خوبی با راهبرد الگوسازی آشنا شوید.
مثال 1) دو عدد طبیعی را به گونه‌ای در نظر بگیرید که حاصل‌ضرب این دو عدد 30 و حاصل جمع آنها کمترین مقدار ممکن باشد؟
حل: برای حل این سوال باید اعداد مختلف را به صورت مرتب و دقیق بنویسیم و عددی از قلم نیفتد. پس برای این کار از جدول زیر استفاده می‌کنیم:
| حاصل جمع | دومین عدد | اولین عدد |
| 31 | 30 | 1 |
| 17 | 15 | 2 |
| 13 | 10 | 3 |
| 11 | 6 | 5 |
با توجه به جدول مشخص است که دو عدد 5 و 6 پاسخ سوال هستند.
مثال 2) با رقم‌های 6 و 4 و 1 تمامی اعداد سه رقمی ممکن را بنویسید (تکرار ارقام مجاز نیست).
حل:
| یکان | دهگان | صدگان |
| 6 | 4 | 1 |
| 4 | 6 | 1 |
| 6 | 1 | 4 |
| 1 | 6 | 4 |
| 1 | 4 | 6 |
| 4 | 1 | 6 |
آنچه در حل این مسائل اهمیت دارد، نظم و ترتیب موجود در پاسخ‌ها می‌باشد. این نظم باعث کاهش درصد خطا در پاسخ به سوالات این چنینی خواهد شد.
راهبرد حذف حالت‌های نامطلوب ریاضی هفتم
همانطور که به شما قول داده بودیم در مقاله آموزش فصل اول ریاضی هفتم کلیه مطالب کتاب درسی را بررسی خواهیم کرد. اکنون به راهبرد حذف حالت‌های نامطلوب رسیدیم. گاهی در مسائل جواب‌هایی بدست می‌آید که نادرست هستند. در واقع در این راهبرد تمامی جواب‌ها را می‌نویسیم و سپس جواب‌های نامطلوب را حذف می‌کنیم. در نتیجه جواب درست باقی خواهد ماند و مسئله حل خواهد شد. برای درک بهتر این روش به مثال زیر توجه کنید.
مثال) مجموع سن سه نفر 16 سال و حاصل‌ضرب سن آنها 90 است. سن بزرگ‌ترین نفر چقدر است؟
حل:
| حاصل جمع | جاصل‌ضرب | نفر سوم | نفر دوم | نفر اول |
| 16 | 80 | 10 | 4 | 2 |
| 16 | 56 | 7 | 8 | 1 |
| 16 | 140 | 7 | 5 | 4 |
| 16 | 90 | 9 | 5 | 2 |
همانطور که از جدول بالا مشخص شد، سن بزرگ‌ترین فرد 9 سال است. در واقع با حذف سه حالت نامطلوب اول به جواب درست رسیدیم.
آموزش فصل اول ریاضی هفتم راهبرد الگویابی
در دوره ابتدایی در درس ریاضی با الگوهای عددی و شکل‌هایی آشنا شدید که رابطه خاصی بین اعداد یا اشکال وجود داشت. یافتن الگو بین اعداد می‌تواند به یافتن پاسخ مسائل کمک حال شما باشد. اکنون در آموزش فصل اول ریاضی هفتم به معرفی راهبرد الگویابی می‌پردازیم. در ادامه هم الگوهای بین اعداد و هم الگوهای بین شکل‌های مختلف را بررسی می‌کنیم. پس به مثال‌های زیر با دقت توجه کنید تا راهبرد الگویابی را به آسانی یاد بگیرید.
مثال 1) رابطه بین اعداد زیر را توضیح دهید و سه عدد بعدی هر الگو را بنویسید.
الف) ….،….،…..،2،6،10،14
ب) ….،….،….،1،3،9،27
ج)….،….،….،320،160،80،40
حل: حالا با کمی دقت الگو مناسب برای هر مورد را می‌توانیم به آسانی بیابیم.
قسمت الف) اعداد به صورت چهار تا چهار تا اضافه می‌شوند. یعنی هر عدد از جمع عدد قبلی با عدد چهار بدست می‌آید ⇐ 18،22،26
قسمت ب) هر عدد از ضرب عدد قبلی در عدد سه بدست می‌آید ⇐ 81،243،729
قسمت ج) رابطه تقسیم بین اعداد وجود دارد. یعنی هر عدد از تقسیم عدد قبلی بر دو بدست می‌آید ⇐ 5،10،20
مثال 2) شکل بیستم الگو زیر از چند دایره تشکیل می‌شود؟
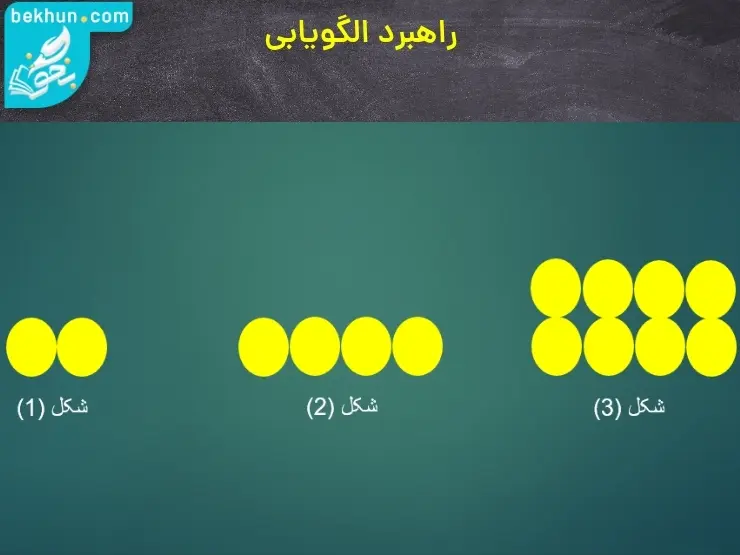حل: از شکل‌ها میتوان پی برد رابطه به صورت مقابل است: شماره شکل به توان 2 = تعداد دایره‌ها ⇐ تعداد دایره شکل بیستم : 400 = 202
راهبرد حدس و آزمایش ریاضی هفتم
در ادامه مطالب آموزش فصل اول ریاضی هفتم به راهبرد حدس و آزمایش می‌رسیم. گاهی اوقات بعضی مسائل جواب طولانی و دشوار دارد. برای رسیدن به پاسخ در این نوع سوالات بهترین کار انجام حدس و آزمایش است. یعنی یک جواب برای مسئله حدس بزنیم سپس بررسی کنیم که این جواب تا چه اندازه با جواب مورد نظر سوال ما فاصله دارد؟ اگر جواب کمتر از جواب سوال بدست آمد، حدس بعدی مقدار بزرگ‌تری خواهد بود و بالعکس. برای درک بهتر راهبرد حدس و آزمایش 2 مثال برای شما حل می‌کنیم.
مثال 1) 30 دستگاه ماشین و موتورسیکلت در یک پارکینگ طبقاتی وجود دارد. اگر تعداد کل چرخ‌ها 100 عدد باشد، چند ماشین و موتورسیکلت در پارکینگ موجود است؟
حل: حدس اولیه خود را با 15 ماشین و 15 موتورسیکلت شروع می‌کنیم و سپس با توجه به پاسخ حدس خود را بیشتر یا کمتر خواهیم کرد.
| بررسی و آزمایش | تعداد موتورسیکلت | تعداد ماشین |
| 90 | 15 | 15 |
| 110 | 5 | 25 |
| 100 | 10 | 20 |
پس همانطور که از جدول مشخص است تعداد ماشین 20 و تعداد موتورسیکلت 10 عدد می‌باشد.
مثال 2) دو زاویه مکمل یکدیگر هستند. اگر اندازه یکی از زاویه‌ها 2 برابر دیگری باشد، این دو زاویه را بیابید.
حل: شما به خوبی می‌دانید که دو زاویه مکمل یعنی مجموع اندازه آنها 180 درجه می‌شود. پس باید دو زاویه را به نحوی انتخاب کنیم که یکی 2 برابر دیگری و مجموع زاویه‌ها 180 درجه شود.
| بررسی و آزمایش | زاویه دوم | زاویه اول |
| 150 | 100 | 50 |
| 210 | 140 | 70 |
| 180 | 120 | 60 |
پس با راهبرد حدس و آزمایش فهمیدیم که اندازه دو زاویه 60 و 120 درجه است.
آموزش فصل اول ریاضی هفتم راهبرد زیر مسئله
در حل بعضی مسائل میتوان با طرح چند مسئله ساده‌تر، مسئله اصلی را به آسانی حل کرد. یعنی شما با طرح سوال‌های درست مسئله را به چندین زیر مسئله تقسیم خواهید کرد. شاید الان به فکر فرو رفته‌اید و با خود می‌گویید: “ای وای حالا با این همه مسئله چیکار کنم؟!!” اصلا نگران نباشید ما در آموزش فصل اول ریاضی هفتم با حل کردن مسائل مختلف نیاز شما را برطرف می‌کنیم.
مثال 1) علی می‌خواهد برای تولد پدرش یک جفت کفش بخرد. او هر هفته 5000 تومان در قلک خود می‌اندازد. پس از 6 هفته علی نصف قیمت کفش را در قلک خود تهیه کرده است. قیمت کفش چقدر است؟
برای حل این سوال ابتدا بیایید با هم به سوالات زیر به ترتیب پاسخ دهیم:
الف) علی پس از 6 هفته چقدر پول در قلک انداخته است؟ خب علی هر هفته 5000 تومان در قلک می‌اندازد پس بعد از 6 هفته داریم: 30000 = 6 × 5000
ب) اگر پس‌انداز علی نصف قیمت کفش باشد، قیمت کفش چقدر است؟ پس‌انداز علی 30000 تومان است پس قیمت کفش برابر است با: 60000 = 2 × 30000
همانطور که مشاهده کردید با حل دو مسئله ساده‌تر به جواب مسئله اصلی رسیدیم.
مثال 2) یک مغازه‌دار 40 بسته ماکارونی به قیمت هر بسته 5000 تومان و 30 عدد نوشابه به قیمت هر عدد 3000 تومان خرید. او هر بسته ماکارونی را 7000 و هر عدد نوشابه را 5000 فروخت. این مغازه‌دار چقدر از فروش خود سود کرده است؟
برای حل این سوال بهتر است ابتدا سوالات زیر را حل کنیم؟
الف) بهای خرید ماکارونی چقدر است؟ تومان 200000 = 5000 × 40
ب) بهای خرید نوشابه چقدر است؟ تومان 90000 = 3000 × 30
ج) کل پول پرداخت شده را محاسبه کنید. تومان 290000 = 90000 + 200000
د) بهای فروش ماکارونی چقدر است؟ تومان 280000 = 7000 × 40
ه) بهای فروش نوشابه چقدر است؟ تومان 150000 = 5000 × 30
و) کل پول فروش اجناس را محاسبه کنید. تومان 430000 = 150000 + 280000
ز) میزان سود این مغازه‌دار چقدر است؟ تومان 140000 = 290000 – 430000
پس برای حل این مسئله با حل چندین زیرمسئله به جواب نهایی رسیدیم.
راهبرد حل مسئله ساده‌تر ریاضی هفتم
گاهی برای حل بعضی مسائل میتوان از حل مسائل ساده‌تر و اعداد تقریبی استفاده کرد. سپس برای حل مسئله اصلی از الگویابی کمک می‌گیریم تا جواب نهایی را بدست بیاوریم. در واقع از جواب مسائل ساده‌تر به جواب مسئله اصلی خواهیم رسید. در مقاله آموزش فصل اول ریاضی هفتم دو نوع نمونه سوال برای راهبرد حل مسئله ساده‌تر در نظر گرفته‌ایم. با حل این مسائل میتوانید به خوبی با راهبرد حل مسئله ساده‌تر آشنا شوید.
مثال 1) حاصل عبارت مقابل را بدست آورید. 99 + …. + 5 + 3 + 1
حل: برای حل این سوال از مجموع اعداد کوچکتر شروع می‌کنیم. همانطور که مشخص است عبارت فوق مجموع اعداد طبیعی فرد کوچکتر از 100 است، پس خواهیم داشت:
1 = 1 ، 1 + 3 = 4 ، 1 + 3 + 5 = 9 ، 1 + 3 + 5 + 7 = 16
همانگونه که مشخص است در هر مرحله یک عدد مربع کامل بدست می‌آید. اگر عدد آخری که جمع می‌شود را 1 – 2n در نظر بگیریم، حاصل مجموع n2 خواهد بود. حال که الگو مناسب را یافتیم به سراغ مسئله اصلی برویم: ? = 99 + …. + 5 + 3 + 1
خب عدد آخر 99 است پس داریم: 99 = 1 – 2n ⇐ با حل معادله خواهیم داشت 50 = n
⇐ حاصل عبارت برابر است با : 2500= 502
مثال 2) ضخامت یک کتاب ریاضی 1/5 سانتی‌متر است. اگر این کتاب 300 صفحه داشته باشد، ضخامت هر برگ کاغذ آن چند سانتی‌متر است؟
حل: ضخامت کتاب را 20 سانتی‌متر و تعداد صفحات کتاب را 8 صفحه در نظر می‌گیریم. چون هر برگ کتاب شامل دو صفحه می‌باشد، پس برگ 4 = 2 ÷ 8 (یعنی یک کتاب 8 صفحه‌ای دارای 4 برگ کاغذ می‌باشد). ضخامت 4 برگ کاغذ 20 سانتی‌متر است، پس 5 = 4 ÷ 20 ضخامت هر برگ 5 سانتی‌متر است.
مطابق راه‌حل مسئله ساده‌تر باید ضخامت کتاب را بر تعداد برگ‌ها تقسیم کنیم: برگ 150 = 2 ÷ 300 صفحه
بنابراین ضخامت هر برگ کاغذ 0/01 سانتی‌متر است. ⇒ 0/01 = 150 ÷ 1/5
آموزش فصل اول ریاضی هفتم راهبرد روش‌های نمادین
آخرین مطلبی که در آموزش فصل اول ریاضی هفتم بررسی می‌شود، راهبرد روش‌های نمادین است. بسیاری از مسئله‌ها را میتوان به زبان ریاضی تبدیل کرد. به این ترتیب که خواسته مسئله را تعیین می‌کنیم و به جای آن مربع قرار می‌دهیم. سپس مسئله را با نمادهای ریاضی به صورت یک تساوی می‌نویسیم. در انتها به کمک راهبرد حدس و آزمایش مقدار مربع را می‌یابیم. برخی مسئله‌ها را نیز میتوان مدل‌سازی کرد و از روش‌های هندسی آن را حل نمود. برای درک بهتر این روش به مسائل حل شده زیر توجه کنید.
مثال 1) امیر 5 شاخه گل از گل‌فروشی خرید. او 20000 تومان به گل فروش داد و 2500 تومان پس گرفت. قیمت هر شاخه گل را محاسبه کنید.
حل: قیمت هر شاخه گل را با علامت مربع در نظر می‌گیریم، بنابراین: 20000 = 2500 + مربع × 5
پس قیمت هر شاخه گل 3500 تومان است.
مثال 2) پارسا و پدرام 64 جلد کتاب را صحافی کرده‌اند. اگر پارسا 12 جلد کتاب بیشتر از پدرام صحافی کرده باشد، هر کدام چند کتاب صحافی کرده‌اند؟
حل: تعداد کتاب‌های صحافی شده پدرام را با مربع نشان می‌دهیم. چون پارسا 12 جلد کتاب بیشتر از پدرام صحافی کرده است، بنابراین تعداد کتاب‌های صحافی شده پارسا (مربع +12) جلد می‌باشد. مسئله را با تساوی زیر نشان می‌دهیم:
64 = مربع + (12 + مربع)
به کمک راهبرد حدس و آزمایش و با توجه به جدول زیر پاسخ مسئله را به راحتی بدست می‌آوریم.
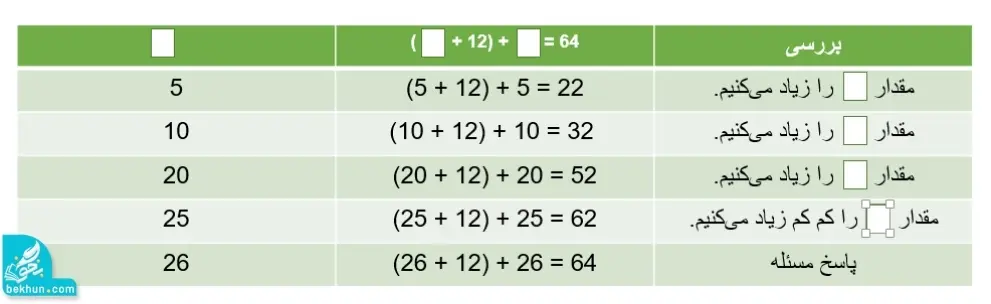از جدول فوق مشخص است که تعداد کتاب‌هایی که پارسا و پدرام جلد کرده‌اند، به ترتیب 38 و 26 جلد است.
سخن پایانی
بخونی‌های عزیز به پایان مقاله آموزش فصل اول ریاضی هفتم رسیدیم. این مقاله آغازی برای تسلط شما در فصل اول ریاضی هفتم است، چرا که تمامی سوالات کتاب را در قالب گام به گام فصل اول ریاضی هفتم حل خواهیم کرد و همچنین با مقاله نمونه سوال فصل اول ریاضی هفتم شما را به تسلط کامل خواهیم رساند. برای مطالعه این مقالات کافیست که به لینک‌های داده شده مراجعه کنید. شما رفقای پایه هفتم میتوانید از طریق لینک آموزش ریاضی هفتم، کلیه مقالات آموزشی ریاضی هفتم را مطالعه کنید و برای مطالعه سایر دروس ریاضی هفتم، لینک قرار داده شده را دنبال کنید. همچنین شما میتوانید مقالات این چنینی برای درس‌های علوم، عربی و ریاضی پایه هفتم را از طریق لینک قرار داده شده را دنبال نمایید.
امیدواریم که مطالب این مقاله مورد توجه شما قرار گرفته باشد و در صورت رضایت با دوستان خود این مقاله را به اشتراک بگذارید. شما میتوانید با عضویت در خبرنامه به تمامی مقالات به صورت کاملا رایگان دسترسی داشته باشید. همچنین با ثبت امتیاز و نوشتن نظرات خود را ما را در هرچه بهتر نوشتن مقالات یاری کنید و باعث دلگرمی ما شوید.
سوالات متداول
- آیا در آموزش فصل اول ریاضی هفتم تمامی مطالب کتاب درسی بررسی شده است؟
بله، در این مقاله کلیه مباحث فصل اول ریاضی هقتم با زبانی ساده بیان شده است. - در آموزش فصل اول ریاضی هفتم سوالات کتاب درسی نیز حل شده است؟
خیر، برای حل سوالات کتاب درسی از مقاله گام به گام فصل اول ریاضی هفتم استفاده کنید. - از چه طریقی میتوان جزوه این فصل از ریاضی هفتم را دریافت کنیم؟
شما میتوانید از قسمت دانلود سایت بخون در انتها مقاله، pdf مطلب را دانلود کنید.
